Условие:
3.241. Найдите длину отрезка MN на рисунке 58, если отрезок BM равен 15 см.
Известно, что если отрезок состоит из нескольких отрезков, то его длина равна сумме длин данных отрезков, то есть искомый отрезок MN равен:
MN=MB+BC+CN=3y+2y+7y.
Согласно распределительному свойству умножения относительно сложения для того, чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения:
(a+b)c=ac+bc.
Воспользуемся данным равенством и запишем, что:
3y+2y+7y=(3+2+7)y
Или, выполнив сложение:
(3+2+7)y=12y (см) – длина отрезка MN.
По условию задачи отрезок BM=15 см.
Из рисунка видно, что BM=3y см.
Значит, можно составить следующее уравнение:
3y=15
Неизвестен множитель y.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим:
y=15:3
Или, выполнив деление:
y=5 (см).
Подставим значение y в полученное выражение, значит длина отрезка MN составит:
12y=12•5=60 (см) – длина отрезка MN.
Ответ: 60 см.
Решение 1 - 3.241 - §3 Умножение и деление натуральных чисел.:
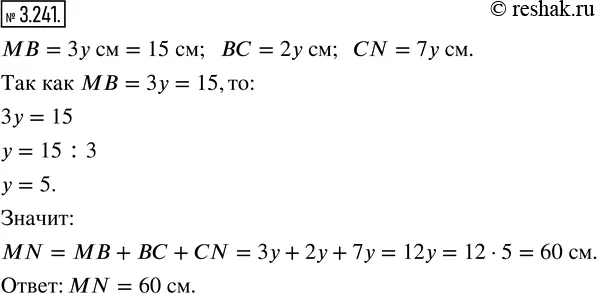
Решение 2 - 3.241:

