Условие:

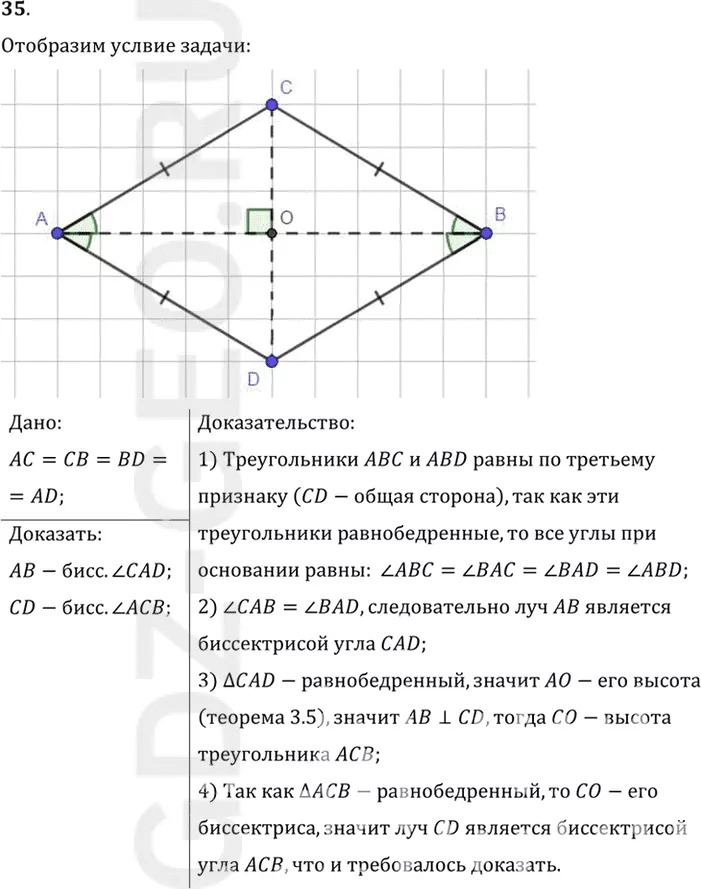
35. Отрезки АВ и CD пересекаются. Докажите, что если отрезки АС, СВ, BD и AD равны, то луч АВ является биссектрисой угла CAD и луч CD — биссектрисой угла АСВ (рис. 66).

Доказательство:

1) Треугольники ABC и ABD равны по третьему

признаку (CD-общая сторона), так как эти

треугольники равнобедренные, то все углы при

основании равны: угол ABC = углу BAC = углу BAD = углу ABD;

2) угол CAB = углу BAD, следовательно луч AB является

биссектрисой угла CAD;

3) треугольник CAD-равнобедренный, значит AO-его высота

(теорема 3.5), значит AB перпендикулярен CD, тогда CO-высота

треугольника ACB;

4) Так как треугольник ACB-равнобедренный, то CO-его

биссектриса, значит луч CD является биссектрисой

угла ACB, что и требовалось доказать.

Развернуть