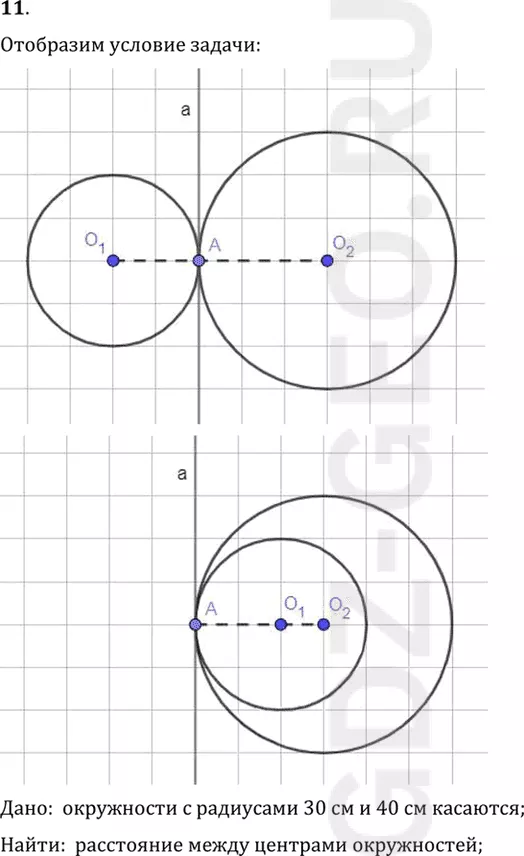
Условие:

11. Окружности с радиусами 30 см и 40 см касаются. Найдите расстояние между центрами окружностей в случаях внешнего и внутреннего касаний.

Дано: окружности с радиусами 30 см и 40 см касаются;

Найти: расстояние между центрами окружностей;

Решение:

1) Пусть a-общая касательная к этим окружностям и A-точка

касания;

2) По свойству касательных a перпендикулярен AO1 и a перпендикулярен AO2, значит прямые, на

которых лежат отрезки AO1 и AO2 параллельны, но они имеют общую

точку A, значит они совпадают;

3) Отрезки O1 A и AO2 лежат на одной прямой, значит искомое расстояние

равно длине отрезка O1 O2;

4) В случае внешнего касания окружностей:

O1 O2=O1 A+AO2=30+40=70 см;

5) В случае внутреннего касания окружностей:

O1 O2=|O1 A-AO2 |=|30-40|=10 см;

Ответ: 10 см.

Развернуть