Условие:

14 1) Окружности с центрами О и O1 пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ООх.

2) Докажите, что две окружности не могут пересекаться более чем в двух точках.

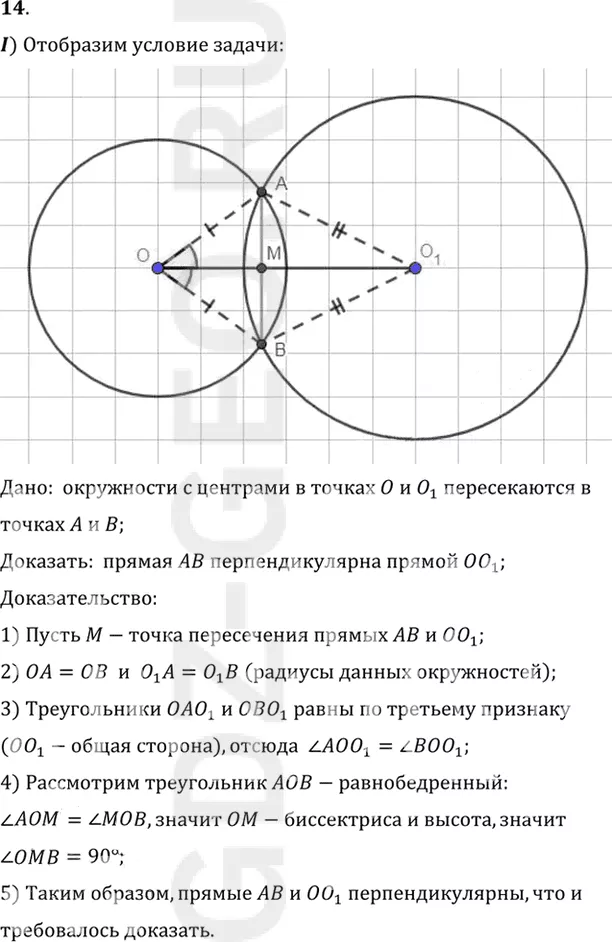
I) Отобразим условие задачи:

Дано: окружности с центрами в точках O и O1 пересекаются в

точках A и B;

Доказать: прямая AB перпендикулярна прямой OO1;

Доказательство:

1) Пусть M-точка пересечения прямых AB и OO1;

2) OA=OB и O1 A=O1 B (радиусы данных окружностей);

3) Треугольники OAO1 и OBO1 равны по третьему признаку

(OO1-общая сторона), отсюда угол AOO1 = углу BOO1;

4) Рассмотрим треугольник AOB-равнобедренный:

угол AOM = углу MOB, значит OM-биссектриса и высота, значит

угол OMB=90°;

5) Таким образом, прямые AB и OO1 перпендикулярны, что и

требовалось доказать.

II)

Доказать: две окружности не могут пересекаться более, чем в двух

точках;

Доказательство:

1) Пусть окружности с центрами в точках O и O1 пересекаются в

точках A и B, тогда из доказанного AB перпендикулярен OO1;

2) Допустим, что окружности пересекаются в третьей точке C,

тогда AC перпендикулярен OO1 и BC перпендикулярен OO1, значит AC||BC;

3) Так как прямые AC и BC имеют общую точку, то они не могут быть

параллельны, значит такой точки C не существует;

4) Таким образом, окружности могут пересекаться не более, чем в

двух точках, что и требовалось доказать.

Развернуть