Условие:

44. Докажите, что: 1) прямые, содержащие высоты данного треугольника, являются серединными перпендикулярами к сторонам треугольника, образованного прямыми, проходящими через вершины данного треугольника параллельно соответствующим противолежащим сторонам; 2) все три прямые, содержащие высоты треугольника, пересекаются в одной точке.

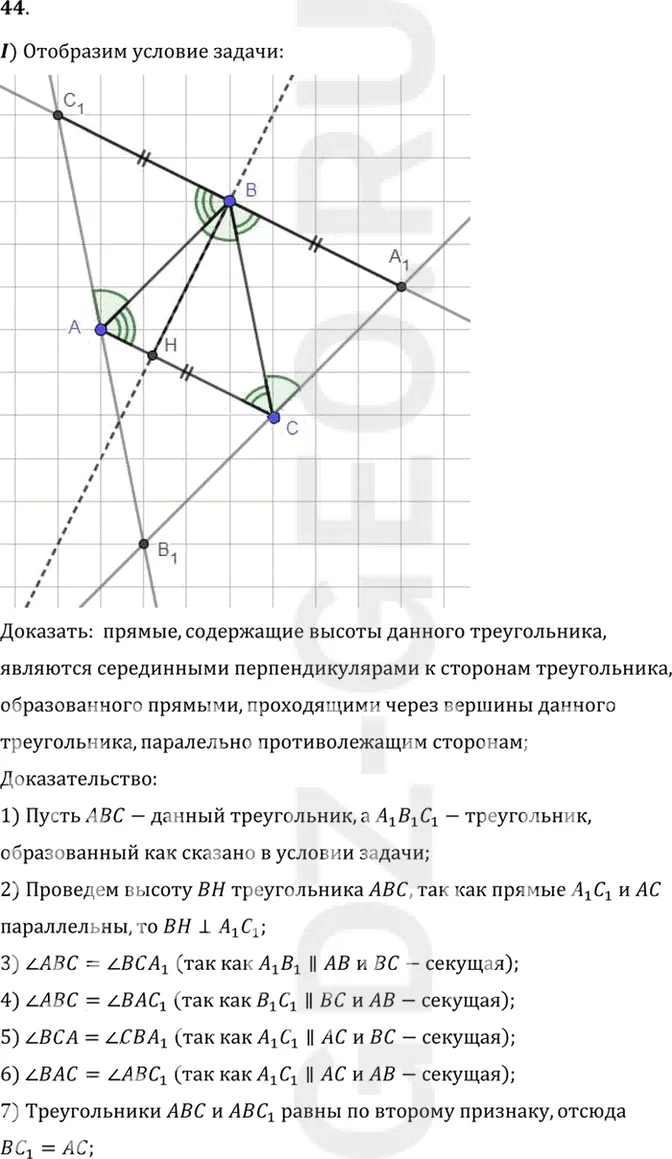
I) Отобразим условие задачи:

Доказать: прямые, содержащие высоты данного треугольника,

являются серединными перпендикулярами к сторонам треугольника,

образованного прямыми, проходящими через вершины данного

треугольника, паралельно противолежащим сторонам;

Доказательство:

1) Пусть ABC-данный треугольник, а A1 B1 C1-треугольник,

образованный как сказано в условии задачи;

2) Проведем высоту BH треугольника ABC, так как прямые A1 C1 и AC

параллельны, то BH перпендикулярен A1 C1;

3) угол ABC = углу BCA1 (так как A1 B1 ||AB и BC-секущая);

4) угол ABC = углу BAC1 (так как B1 C1 ||BC и AB-секущая);

5) угол BCA = углу CBA1 (так как A1 C1 ||AC и BC-секущая);

6) угол BAC = углу ABC1 (так как A1 C1 ||AC и AB-секущая);

7) Треугольники ABC и ABC1 равны по второму признаку, отсюда

BC1=AC;

8) Треугольники ABC и CBA1 равны по второму признаку, отсюда

BA1=AC;

9) Таким образом, C1 B=BA1, значит прямая BH является серединным

перпендикуляром стороны A1 C1 треугольника A1 B1 C1, что и требовалось

Доказать.

10) Аналогичным образом доказывается и для других высот и сторон;

II)

Доказать: все три прямые, содержащие высоты треугольника,

пересекаются в одной точке;

Доказательство:

1) Из доказанного в пункте I этой задачи следует, что высоты

треугольнка ABC являются серединными перпендикулярами сторон

треугольника A1 B1 C1;

2) Как было доказано в предыдущей задаче вокруг любого треугольника

можно описать окружность и только одну;

3) Значит высоты треугольника ABC пересекаются в одной точке,

которая является центром описанной около треугольника A1 B1 C1

окружности, что и требовалось доказать.