Условие:

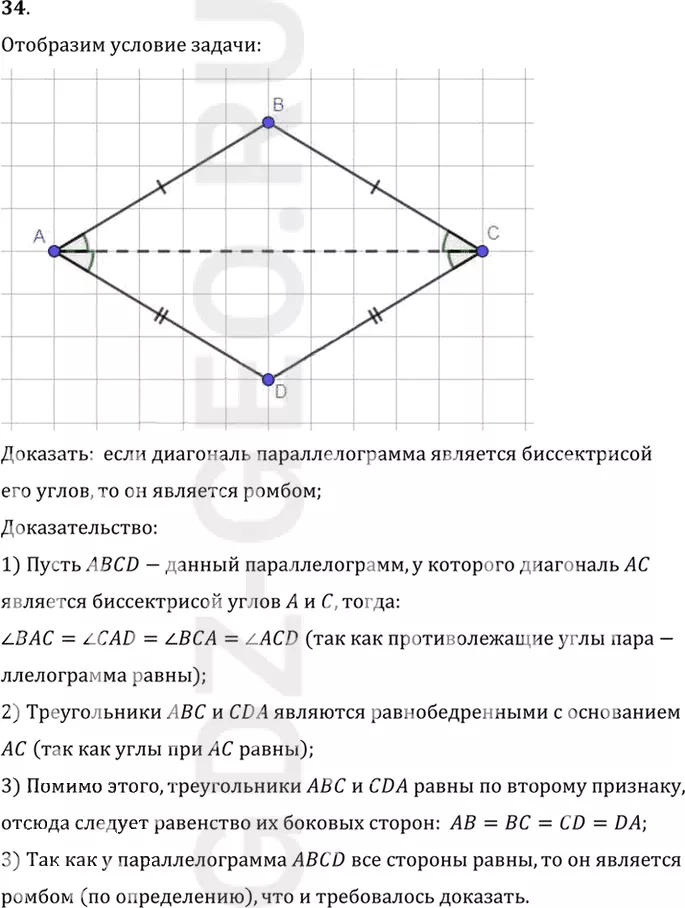
34. Докажите, что если диагональ параллелограмма является биссектрисой его углов, то он является ромбом.

Доказать: если диагональ параллелограмма является биссектрисой

его углов, то он является ромбом;

Доказательство:

1) Пусть ABCD-данный параллелограмм, у которого диагональ AC

является биссектрисой углов A и C, тогда:

угол BAC = углу CAD = углу BCA = углу ACD (так как противолежащие углы пара-

ллелограмма равны);

2) Треугольники ABC и CDA являются равнобедренными с основанием

AC (так как углы при AC равны);

3) Помимо этого, треугольники ABC и CDA равны по второму признаку,

отсюда следует равенство их боковых сторон: AB=BC=CD=DA;

3) Так как у параллелограмма ABCD все стороны равны, то он является

ромбом (по определению), что и требовалось доказать.

Развернуть