Условие:

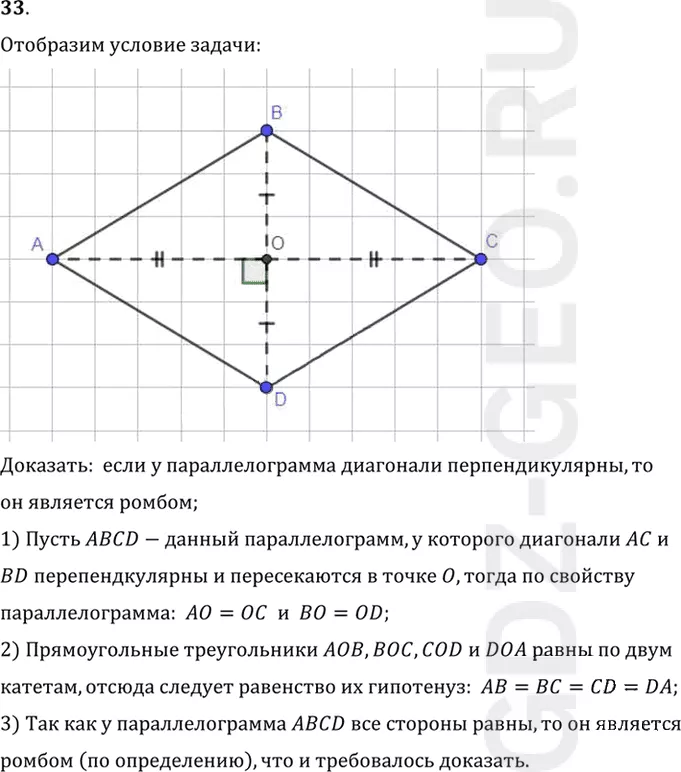
33. Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом.

Доказать: если у параллелограмма диагонали перпендикулярны, то

он является ромбом;

1) Пусть ABCD-данный параллелограмм, у которого диагонали AC и

BD перепендкулярны и пересекаются в точке O, тогда по свойству

параллелограмма: AO=OC и BO=OD;

2) Прямоугольные треугольники AOB, BOC, COD и DOA равны по двум

катетам, отсюда следует равенство их гипотенуз: AB=BC=CD=DA;

3) Так как у параллелограмма ABCD все стороны равны, то он является

ромбом (по определению), что и требовалось доказать.

Развернуть