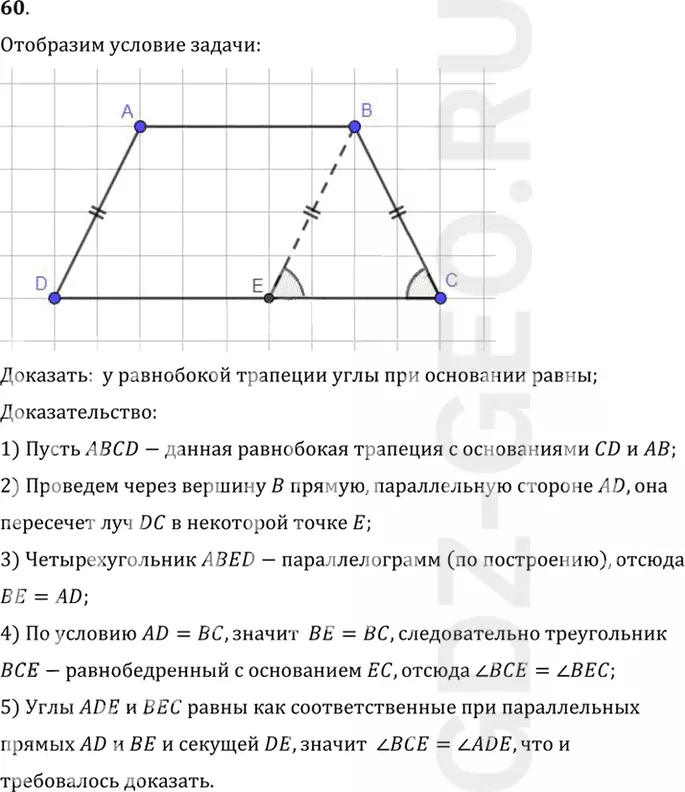
Условие:

60. Докажите, что у равнобокой трапеции углы при основании равны.

Доказать: у равнобокой трапеции углы при основании равны;

Доказательство:

1) Пусть ABCD-данная равнобокая трапеция с основаниями CD и AB;

2) Проведем через вершину B прямую, параллельную стороне AD, она

пересечет луч DC в некоторой точке E;

3) Четырехугольник ABED-параллелограмм (по построению), отсюда

BE=AD;

4) По условию AD=BC, значит BE=BC, следовательно треугольник

BCE-равнобедренный с основанием EC, отсюда угол BCE = углу BEC;

5) Углы ADE и BEC равны как соответственные при параллельных

прямых AD и BE и секущей DE, значит угол BCE = углу ADE, что и

требовалось доказать.

Развернуть