Условие:

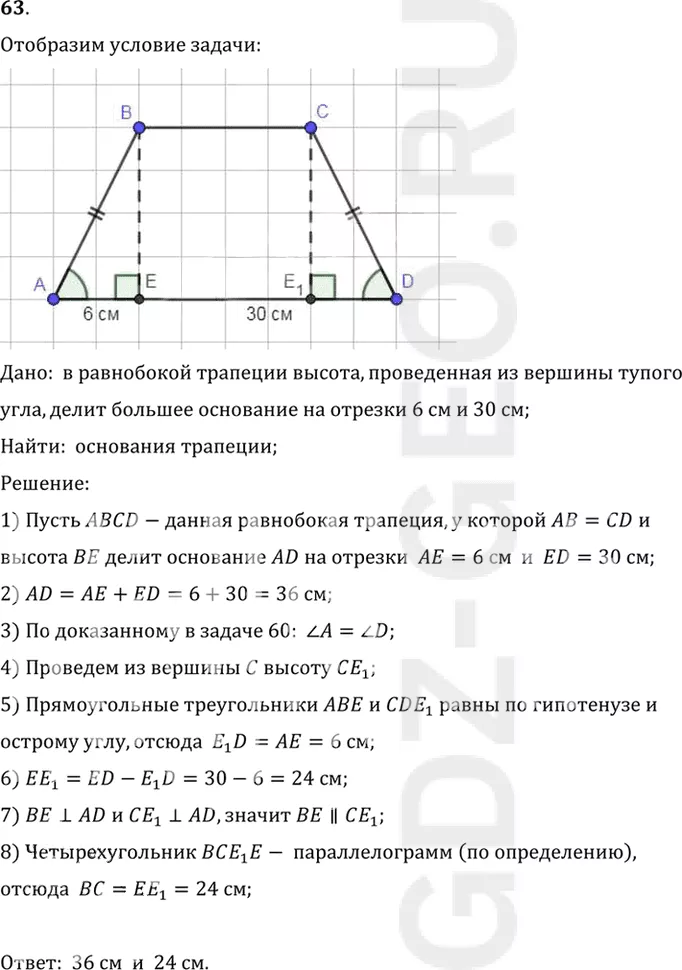
63. В равнобокой трапеции высота, проведённая из вершины тупого угла, делит большее основание на отрезки 6 см и 30 см. Найдите основания трапеции.

Дано: в равнобокой трапеции высота, проведенная из вершины тупого

угла, делит большее основание на отрезки 6 см и 30 см;

Найти: основания трапеции;

Решение:

1) Пусть ABCD-данная равнобокая трапеция, у которой AB=CD и

высота BE делит основание AD на отрезки AE=6 см и ED=30 см;

2) AD=AE+ED=6+30=36 см;

3) По доказанному в задаче 60: угол A = углу D;

4) Проведем из вершины C высоту CE1;

5) Прямоугольные треугольники ABE и CDE1 равны по гипотенузе и

острому углу, отсюда E1 D=AE=6 см;

6) EE1=ED-E1 D=30-6=24 см;

7) BE перпендикулярен AD и CE1 перпендикулярен AD, значит BE||CE1;

8) Четырехугольник BCE1 E- параллелограмм (по определению),

отсюда BC=EE1=24 см;

Ответ: 36 см и 24 см.

Развернуть