Условие:

36. Могут ли пересекаться окружности, центры которых находятся на расстоянии 20 см, а радиусы равны 8 см и 11 см? Объясните ответ.

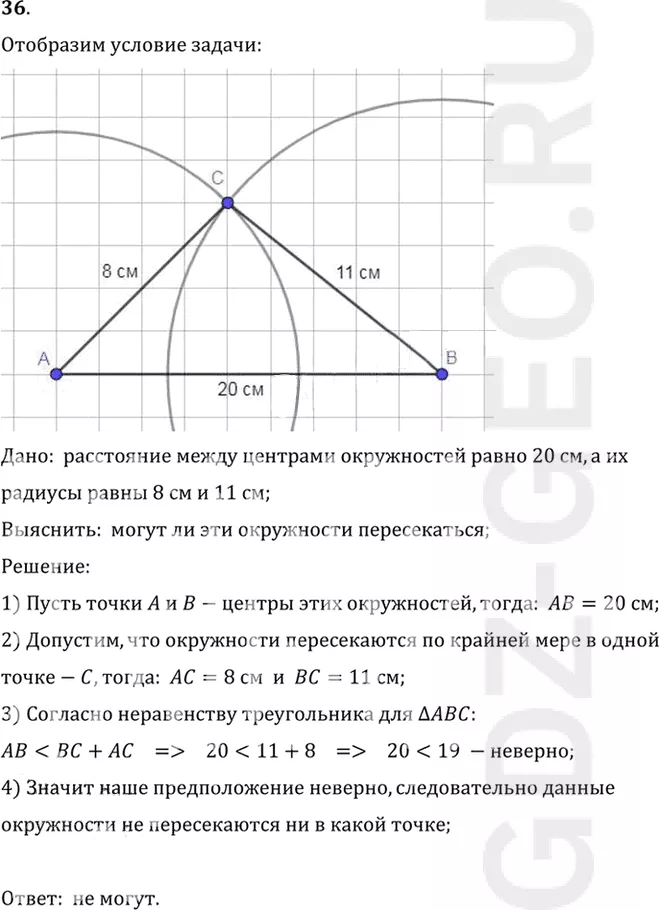
Дано: расстояние между центрами окружностей равно 20 см, а их

радиусы равны 8 см и 11 см;

Выяснить: могут ли эти окружности пересекаться;

Решение:

1) Пусть точки A и B-центры этих окружностей, тогда: AB=20 см;

2) Допустим, что окружности пересекаются по крайней мере в одной

точке-C, тогда: AC=8 см и BC=11 см;

3) Согласно неравенству треугольника для треугольник ABC:

AB 20<11+8 => 20<19 -неверно;

4) Значит наше предположение неверно, следовательно данные

окружности не пересекаются ни в какой точке;

Ответ: не могут.

Развернуть