Условие:

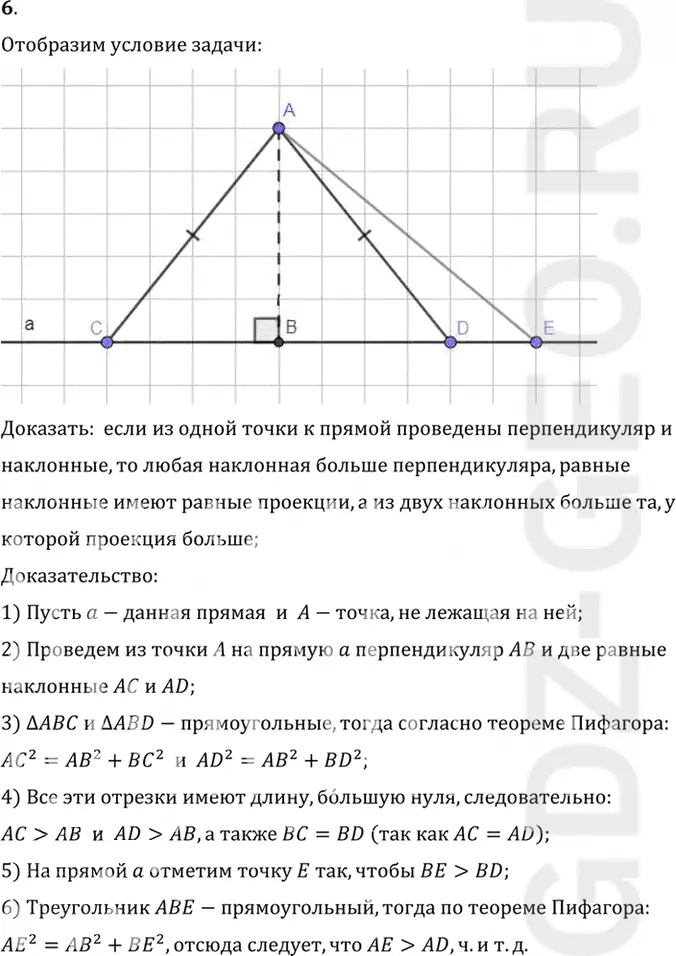
6. Докажите, что если из одной точки к прямой проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра. Равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.

Доказать: если из одной точки к прямой проведены перпендикуляр и

наклонные, то любая наклонная больше перпендикуляра, равные

наклонные имеют равные проекции, а из двух наклонных больше та, у

которой проекция больше;

Доказательство:

1) Пусть a-данная прямая и A-точка, не лежащая на ней;

2) Проведем из точки A на прямую a перпендикуляр AB и две равные

наклонные AC и AD;

3) треугольник ABC и треугольник ABD-прямоугольные, тогда согласно теореме Пифагора:

AC^2=AB^2+BC^2 и AD^2=AB^2+BD^2;

4) Все эти отрезки имеют длину, большую нуля, следовательно:

AC>AB и AD>AB, а также BC=BD (так как AC=AD);

5) На прямой a отметим точку E так, чтобы BE>BD;

6) Треугольник ABE-прямоугольный, тогда по теореме Пифагора:

AE^2=AB^2+BE^2, отсюда следует, что AE>AD, ч.и т.д.