Условие:

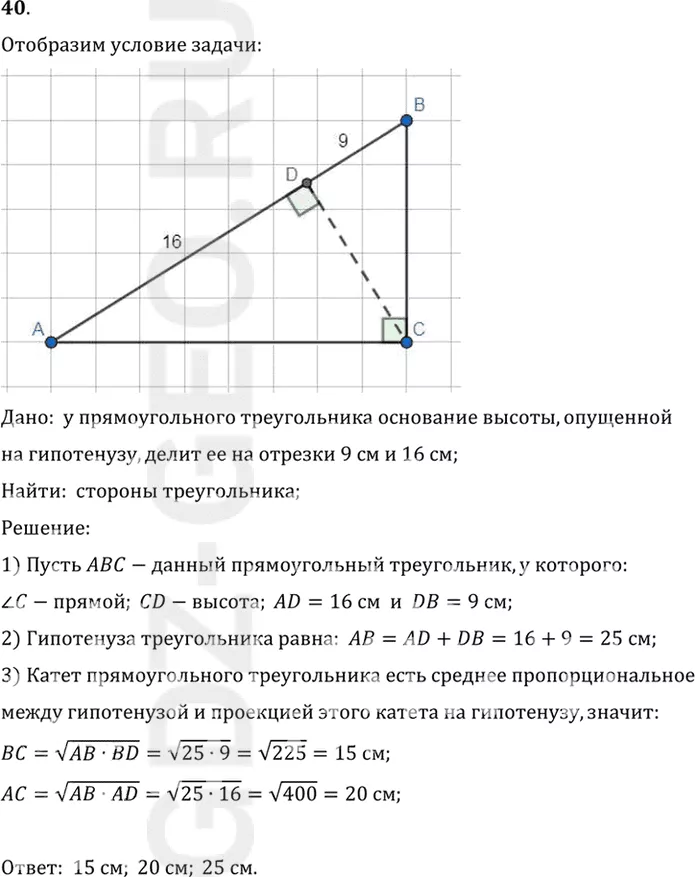
40. Основание высоты прямоугольного треугольника, опущенной на гипотенузу, делит её на отрезки 9 см и 16 см. Найдите стороны треугольника.

Дано: у прямоугольного треугольника основание высоты, опущенной

на гипотенузу, делит ее на отрезки 9 см и 16 см;

Найти: стороны треугольника;

Решение:

1) Пусть ABC-данный прямоугольный треугольник, у которого:

угол C-прямой; CD-высота; AD=16 см и DB=9 см;

2) Гипотенуза треугольника равна: AB=AD+DB=16+9=25 см;

3) Катет прямоугольного треугольника есть среднее пропорциональное

между гипотенузой и проекцией этого катета на гипотенузу.

Развернуть