Условие:

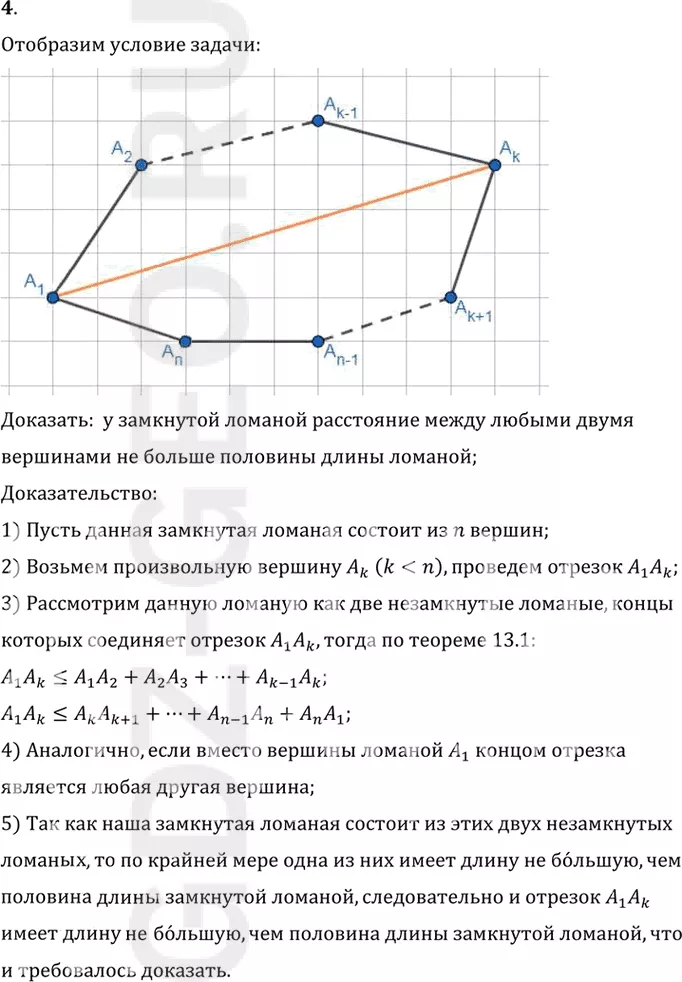
4. Докажите, что у замкнутой ломаной расстояние между любыми двумя вершинами не больше половины длины ломаной.

Доказать: у замкнутой ломаной расстояние между любыми двумя

вершинами не больше половины длины ломаной;

Доказательство:

1) Пусть данная замкнутая ломаная состоит из n вершин;

2) Возьмем произвольную вершину Ak (k< div>

3) Рассмотрим данную ломаную как две незамкнутые ломаные, концы

которых соединяет отрезок A1 Ak, тогда по теореме 13.1:

A1 Ak?A1 A2+A2 A3+...+A(k-1) Ak;

A1 Ak?Ak A(k+1)+...+A(n-1) An+An A1;

4) Аналогично, если вместо вершины ломаной A1 концом отрезка

является любая другая вершина;

5) Так как наша замкнутая ломаная состоит из этих двух незамкнутых

ломаных, то по крайней мере одна из них имеет длину не большую, чем

половина длины замкнутой ломаной, следовательно и отрезок A1 Ak

имеет длину не большую, чем половина длины замкнутой ломаной, что

и требовалось доказать.

Развернуть