Условие:

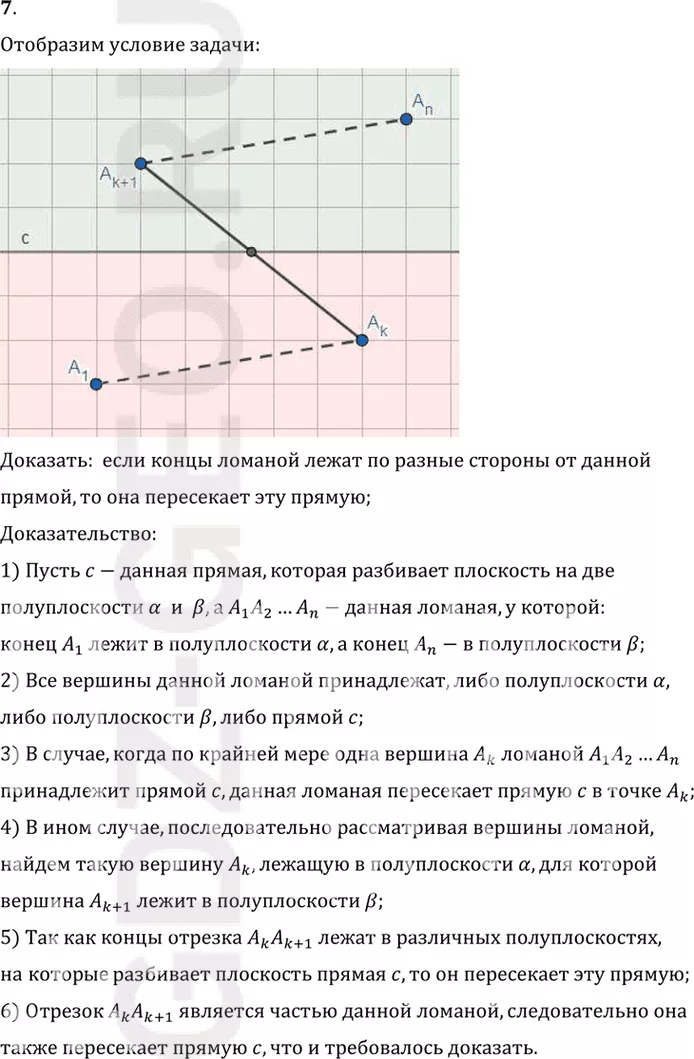
7. Докажите, что если концы ломаной лежат по разные стороны от данной прямой, то она пересекает эту прямую (рис. 294).

Доказать: если концы ломаной лежат по разные стороны от данной

прямой, то она пересекает эту прямую;

Доказательство:

1) Пусть c-данная прямая, которая разбивает плоскость на две

полуплоскости Альфа и Бетта, а A1 A2…An-данная ломаная, у которой:

конец A1 лежит в полуплоскости Альфа, а конец An-в полуплоскости Бетта;

2) Все вершины данной ломаной принадлежат, либо полуплоскости Альфа,

либо полуплоскости Бетта, либо прямой c;

3) В случае, когда по крайней мере одна вершина Ak ломаной A1 A2…An

принадлежит прямой c, данная ломаная пересекает прямую c в точке Ak;

4) В ином случае, последовательно рассматривая вершины ломаной,

найдем такую вершину Ak, лежащую в полуплоскости Альфа, для которой

вершина A(k+1) лежит в полуплоскости Бетта;

5) Так как концы отрезка Ak A(k+1) лежат в различных полуплоскостях,

на которые разбивает плоскость прямая c, то он пересекает эту прямую;

6) Отрезок Ak A(k+1) является частью данной ломаной, следовательно она

также пересекает прямую c, что и требовалось доказать.

Развернуть