Условие:

6. Выведите формулу суммы углов выпуклого многоугольника.

Вывести: формулу суммы углов выпуклого многоугольника;

Решение:

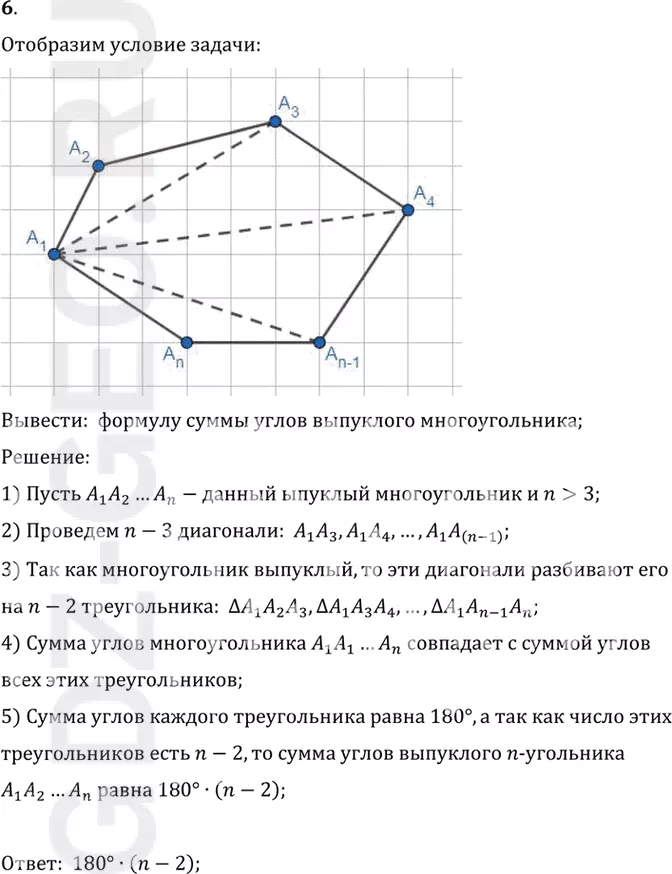
1) Пусть A1 A2…An-данный ыпуклый многоугольник и n>3;

2) Проведем n-3 диагонали: A1 A3, A1 A4, …, A1 A((n-1));

3) Так как многоугольник выпуклый, то эти диагонали разбивают его

на n-2 треугольника: треугольник A1 A2 A3, A1 A3 A4, …, треугольник A1 A(n-1) An;

4) Сумма углов многоугольника A1 A1…An совпадает с суммой углов

всех этих треугольников;

5) Сумма углов каждого треугольника равна 180°, а так как число этих

треугольников есть n-2, то сумма углов выпуклого n-угольника

A1 A2…An равна 180°•(n-2);

Ответ: 180°•(n-2);

Развернуть