Условие:

12. Как построить правильный выпуклый шестиугольник? треугольник? четырёхугольник? восьмиугольник?

Построить: правильный выпуклый шестиугольник, треугольник,

четырехугольник, восьмиугольник;

Построение:

Для построения правильного многоугольника, вписанного в окружность,

достаточно построить его центральный угол;

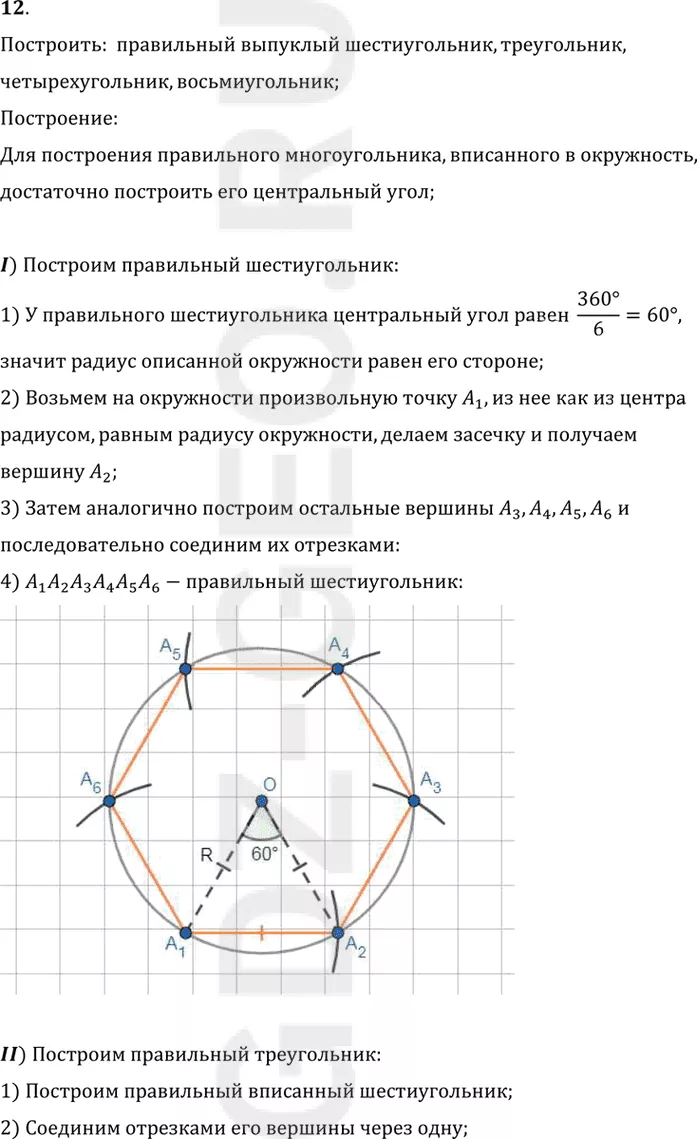
I) Построим правильный шестиугольник:

1) У правильного шестиугольника центральный угол равен (360°)/6=60°,

значит радиус описанной окружности равен его стороне;

2) Возьмем на окружности произвольную точку A1, из нее как из центра

радиусом, равным радиусу окружности, делаем засечку и получаем

вершину A2;

3) Затем аналогично построим остальные вершины A3, A4, A5, A6 и

последовательно соединим их отрезками:

4) A1 A2 A3 A4 A5 A6-правильный шестиугольник:

II) Построим правильный треугольник:

1) Построим правильный вписанный шестиугольник;

2) Соединим отрезками его вершины через одну;

3) A1 A3 A5-правильный треугольник:

III) Построим правильный четырехугольник (квадрат):

1) У квадрата центральный угол равен (360°)/4=90°, значит его диагонали

перпендикулярны;

2) Построим диаметр окружности AC и через центр O окружности

проведем перпендикулярную ему прямую, которая пересечет окружность

в точках B и D;

3) Последовательно соединим точки A, B, C и D отрезками;

4) ABCD-квадрат.

IV) Построим правильный восьмиугольник:

1) Построим правильный вписанный четырехугольник A1 A3 A5 A7;

2) Для сторон A1 A3 и A3 A5 построим серединные перпендикуляры и

отметим точки A2, A4, A6 и A8 на пересечениях этих перпендикуляров

с окружностью;

3) Последовательно соединим точки A1, A2, A3, A4, A5, A6, A7, A8 отрезками;

4) A1 A2 A3 A4 A5 A6 A7 A8-правильный восьмиугольник

Развернуть