Условие:

2. Докажите, что площадь прямоугольника равна произведению его сторон.

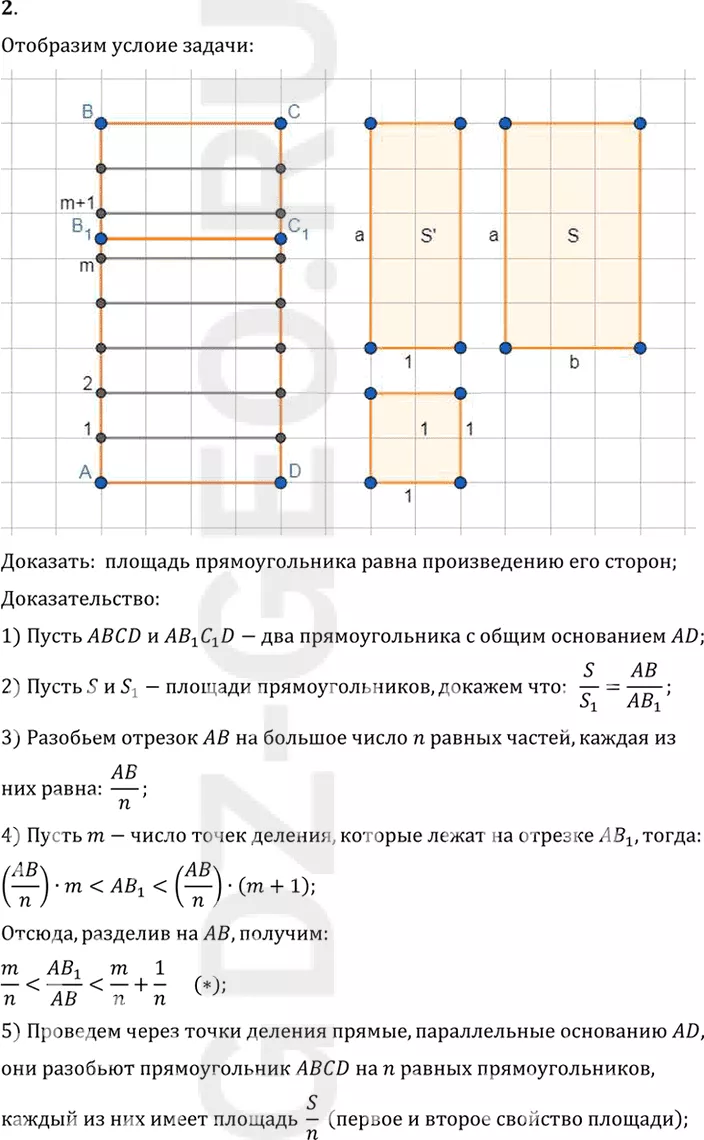
Доказать: площадь прямоугольника равна произведению его сторон;

Доказательство:

1) Пусть ABCD и AB1 C1 D-два прямоугольника с общим основанием AD;

2) Пусть S и S1-площади прямоугольников, докажем что: S/S1 =AB/(AB1 );

3) Разобьем отрезок AB на большое число n равных частей, каждая из

них равна: AB/n;

4) Пусть m-число точек деления, которые лежат на отрезке AB1, тогда:

(AB/n)•m<(AB n)•(m+1); < div>

Отсюда, разделив на AB, получим:

m/n<(AB1)/AB< div>

5) Проведем через точки деления прямые, параллельные основанию AD,

они разобьют прямоугольник ABCD на n равных прямоугольников,

каждый из них имеет площадь S/n (первое и второе свойство площади);

6) Прямоугольник AB1 C1 D содержит первые m прямоугольников, считая

от основния AD, и содержится в (m+1) прямоугольниках, поэтому:

(S/n)•m<(S n)•(m+1 ); < div>

Отсюда, разделив на S1, получим:

m/n< div>

7) Из неравенств (*) и (**) следует, что оба числа (AB1)/AB и S1/S заключены

между числами m/n и m/n+1/n, поэтому они отличаются не более чем на 1/n;

8) Так как n можно взять сколь угодно большим, то это различие может

быть сколь угодно малым, поэтому: (AB1)/AB=S1/S;

9) Возьмем квадрат, являющийся единицей площади, прямоугольник

со сторонами 1 и a, а также прямоугольник со сторонами a и b;

11) Сравнивая их площади, по доказанному будем иметь:

S'/1=a/1 и S/S' =b/1;

12) Перемножая эти равенства почленно, получим:

S'/1•S/S' =a/1•b/1 => S=ab, что и требовалось доказать.

Развернуть