Условие:

3. Докажите, что площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.

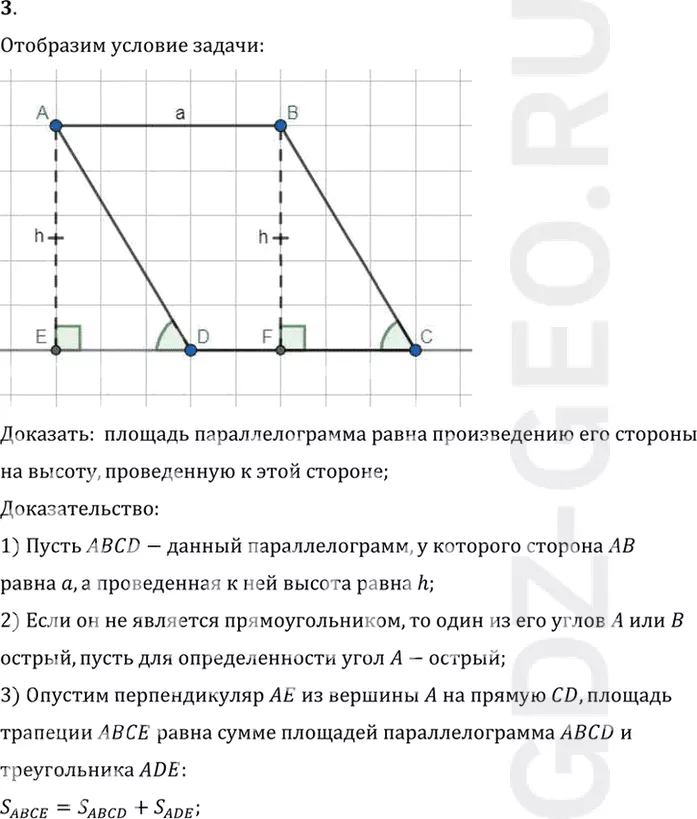
Доказать: площадь параллелограмма равна произведению его стороны

на высоту, проведенную к этой стороне;

Доказательство:

1) Пусть ABCD-данный параллелограмм, у которого сторона AB

равна a, а проведенная к ней высота равна h;

2) Если он не является прямоугольником, то один из его углов A или B

острый, пусть для определенности угол A-острый;

3) Опустим перпендикуляр AE из вершины A на прямую CD, площадь

трапеции ABCE равна сумме площадей параллелограмма ABCD и

треугольника ADE:

SABCE=SABCD+SADE;

4) Опустим перпендикуляр BF из вершины B на прямую CD, тогда

площадь трапеции ABCE равна сумме площадей прямоугольника ABFE

и треугольника BCF:

SABCE=SABFE+SBCF;

5) Так как отрезки AE и BF равны расстоянию между параллельными

прямыми AB и CD, то они являются высотами параллелограмма ABCD,

опущенными на сторону AB:

AE=BF=h;

6) Рассмотрим параллельные прямые AD и BC и секущую DC:

угол ADE=угол BCF (как соответстенные углы);

7) Тогда прямоугольные треугольники ADE и BCF равны по катету и

противолежащему острому углу, значит они имеют равные площади:

SADE=SBCF;

8) Значит площади параллелограмма ABCD и прямоугольника ABFE

равны, то есть:

SABCD=SABFE=AB•BF=a•h, что и требовалось доказать.

Развернуть