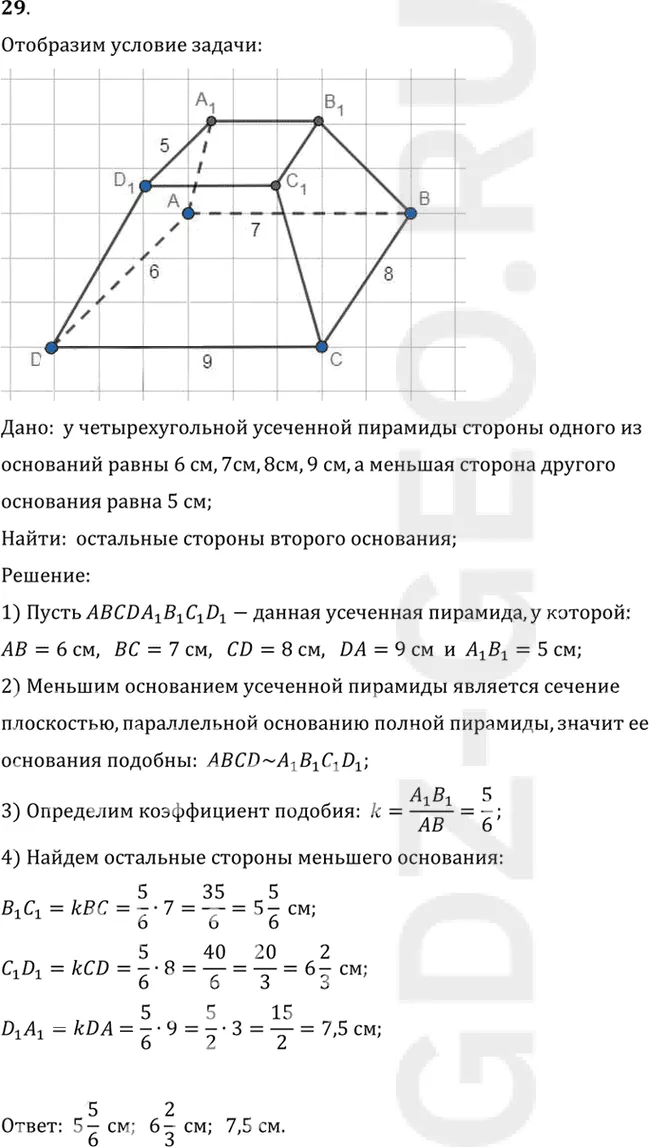
Условие:

29. У четырёхугольной усечённой пирамиды стороны одного основания равны 6 см, 7 см, 8 см, 9 см, а меньшая сторона другого основания равна 5 см. Найдите остальные стороны этого основания.

Дано: у четырехугольной усеченной пирамиды стороны одного из

оснований равны 6 см, 7см, 8см, 9 см, а меньшая сторона другого

основания равна 5 см;

Найти: остальные стороны второго основания;

Решение:

1) Пусть ABCDA1 B1 C1 D1-данная усеченная пирамида, у которой:

AB=6 см, BC=7 см, CD=8 см, DA=9 см и A1 B1=5 см;

2) Меньшим основанием усеченной пирамиды является сечение

плоскостью, параллельной основанию полной пирамиды, значит ее

основания подобны: ABCD~A1 B1 C1 D1;

3) Определим коэффициент подобия: k=(A1 B1)/AB=5/6;

4) Найдем остальные стороны меньшего основания:

B1 C1=kBC=5/6•7=35/6=5 5/6 см;

C1 D1=kCD=5/6•8=40/6=20/3=6 2/3 см;

D1 A1=kDA=5/6•9=5/2•3=15/2=7,5 см;

Ответ: 5 5/6 см; 6 2/3 см; 7,5 см.

Развернуть