Условие:
5.278. Найдите сумму:
а) 7 + 2 5/8; б) 9 1/9 + 20; в) 64 1/7 + 4 4/7; г) 7 5/7 + 4 1/7.
При выполнении вычислений опираемся на следующее правило:
- для того, чтобы найти сумму двух смешанных чисел, необходимо отдельно сложить их целые и дробные части.
а) 7+2 5/8=7+2+5/8=9+5/8=9 5/8
б) 9 1/9+20=9+1/9+20=29+1/9=29 1/9
в) 64 1/7+4 4/7=64+4+1/7+4/7=68+(1+4)/7=68 5/7
г) 7 5/7+4 3/7=7+4+5/7+3/7=11+(5+3)/7=11 8/7=11+1 1/7=12 1/7
Если при сложении смешанных чисел получается неправильная дробь, то выделяем из этой неправильной дроби целую часть и продолжаем сложение.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, то есть выделить целую часть, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель дробной части.
При выделении целой части из неправильной дроби 8/7 используем то, что 8:7=1 (ост.1).
Решение 1 - 5.278 - §5 Обыкновенные дроби:
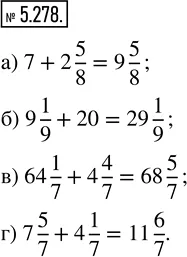
Решение 2 - 5.278:

