Условие:
5.424. Периметр треугольника АВС равен 17/20 м. Сторона АВ равна 17/50 м, сторона ВС на 9/50 м короче АВ. Найдите длину стороны АС.
Сторона AB треугольника равна 17/50 м, а сторона BC – на 9/50 м короче. Значит, сторона BC равна:
17/50-9/50=(17-9)/50=8/50 (м) – сторона BC.
Периметр треугольника равен сумме длин всех его сторон, то есть периметр искомого треугольника равен:
P=AB+BC+AC.
При этом известно, что периметр треугольника ABC равен 17/20 м.
Подставим в формулу длины известных сторон, получим
17/50+8/50+AC=17/20
Или, выполнив сложение,
(17+8)/50+AC=17/20
25/50+AC=17/20
Сократим дробь.
(25•1)/(25•2)+AC=17/20
1/2+AC=17/20
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
AC=17/20-1/2
Приведём дроби к общему знаменателю – 20.
AC=17/20-(1•10)/(2•10)
AC=17/20-10/20
AC=(17-10)/20
AC=7/20 (м) – длина стороны AC.
Ответ: 7/20 м.
Решение 1 - 5.424 - §5 Обыкновенные дроби:
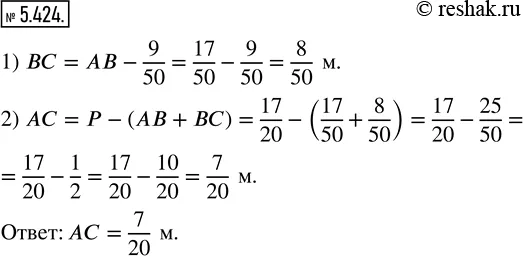
Решение 2 - 5.424:

