Условие:
6.147. Укажите два числа, которые на координатном луче расположены между числами:
а) 5,6 и 5,7; б) 0,2 и 0,3; в) 0 и 0,002; г) 5,2 и 5,21.
Если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной.
При сравнении десятичных дробей опираемся на правило, согласно которому – из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение).
а) 5,6=5,60 и 5,7=5,70.
Значит, числа 5,63 и 5,68 расположены между числами 5,6 и 5,7, так как 5,60<5,63<5,70 и 5,60<5,68<5,70.
б) 0,2=0,20 и 0,3=0,30.
Значит, числа 0,23 и 0,29 расположены между числами 0,2 и 0,3, так как 0,20<0,23<0,30 и 0,20<0,29<0,30.
в) 0=0,0000 и 0,002=0,0020.
Значит, числа 0,0001 и 0,0005 расположены между числами 0 и 0,002, так как 0,0000<0,0001<0,0020 и
0,0000<0,0005<0,0020.
г) 5,2=5,200 и 5,21=5,210.
Значит, числа 5,202 и 5,206 расположены между числами 5,2 и 5,21, так как 5,200<5,202<5,210 и 5,200<5,206<5,210.
Решение 1 - 6.147 - §6 Десятичные дроби:
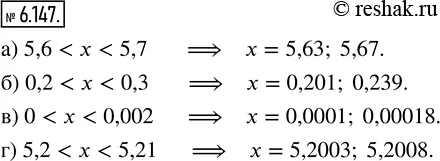
Решение 2 - 6.147:

