Условие:

55. Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма.

Доказать: середины сторон четырехугольника являются вершинами

параллелограмма;

Доказательство:

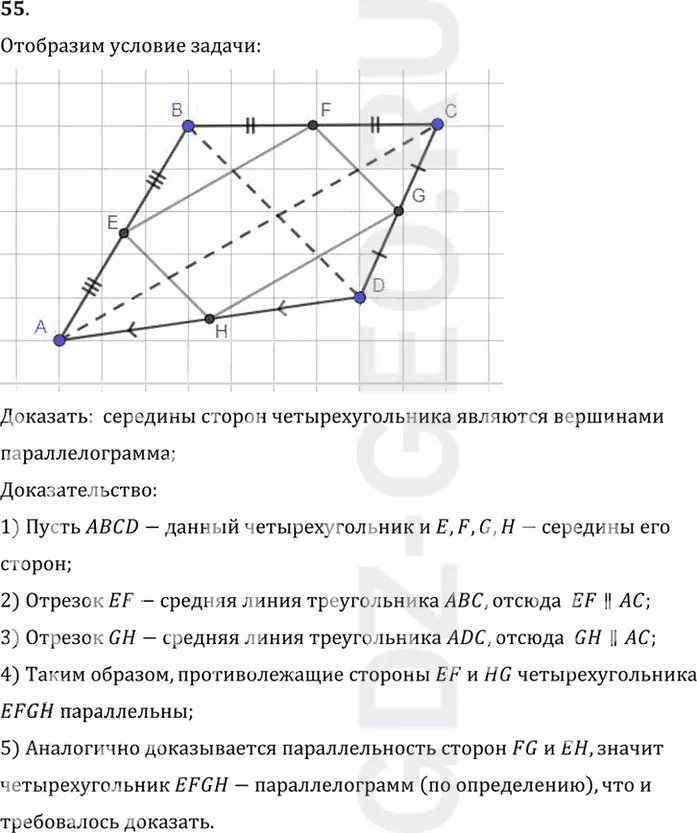
1) Пусть ABCD-данный четырехугольник и E, F, G, H-середины его

сторон;

2) Отрезок EF-средняя линия треугольника ABC, отсюда EF||AC;

3) Отрезок GH-средняя линия треугольника ADC, отсюда GH||AC;

4) Таким образом, противолежащие стороны EF и HG четырехугольника

EFGH параллельны;

5) Аналогично доказывается параллельность сторон FG и EH, значит

четырехугольник EFGH-параллелограмм (по определению), что и

требовалось доказать.

Развернуть