Условие:

15. Докажите теорему Фалеса.

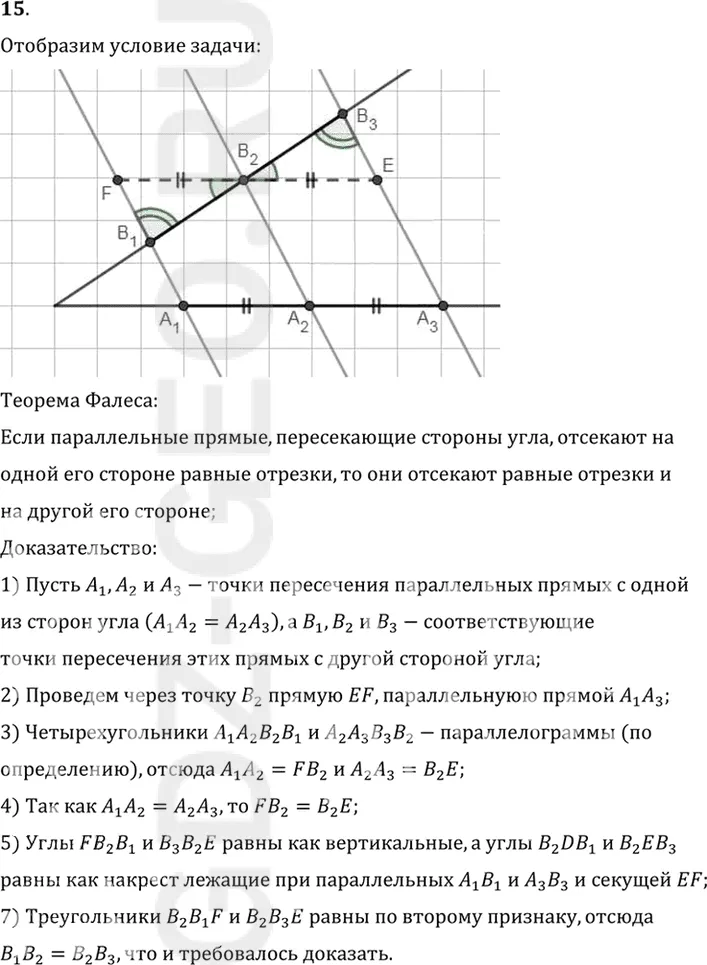
Теорема Фалеса:

Если параллельные прямые, пересекающие стороны угла, отсекают на

одной его стороне равные отрезки, то они отсекают равные отрезки и

на другой его стороне;

Доказательство:

1) Пусть A1, A2 и A3-точки пересечения параллельных прямых с одной

из сторон угла (A1 A2=A2 A3), а B1, B2 и B3-соответствующие

точки пересечения этих прямых с другой стороной угла;

2) Проведем через точку B2 прямую EF, параллельнуюю прямой A1 A3;

3) Четырехугольники A1 A2 B2 B1 и A2 A3 B3 B2-параллелограммы (по

определению), отсюда A1 A2=FB2 и A2 A3=B2 E;

4) Так как A1 A2=A2 A3, то FB2=B2 E;

5) Углы FB2 B1 и B3 B2 E равны как вертикальные, а углы B2 DB1 и B2 EB3

равны как накрест лежащие при параллельных A1 B1 и A3 B3 и секущей EF;

7) Треугольники B2 B1 F и B2 B3 E равны по второму признаку, отсюда

B1 B2=B2 B3, что и требовалось доказать.

Развернуть