Условие:

28. Докажите, что медиана треугольника ABC, проведённая из вершины А, меньше полусуммы сторон АВ и АС.

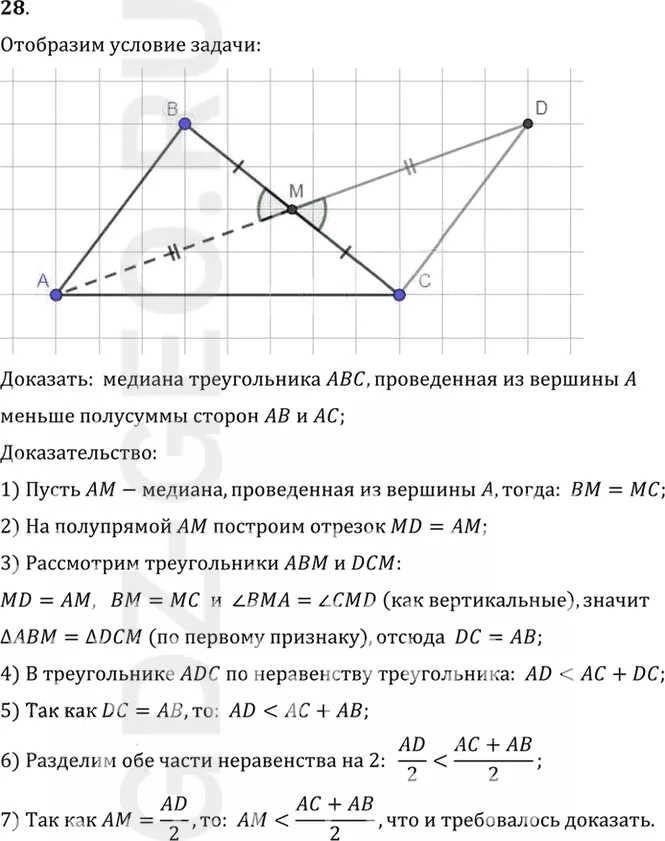
Доказать: медиана треугольника ABC, проведенная из вершины A

меньше полусуммы сторон AB и AC;

Доказательство:

1) Пусть AM-медиана, проведенная из вершины A, тогда: BM=MC;

2) На полупрямой AM построим отрезок MD=AM;

3) Рассмотрим треугольники ABM и DCM:

MD=AM, BM=MC и угол BMA = углу CMD (как вертикальные), значит

треугольник ABM=треугольник DCM (по первому признаку), отсюда DC=AB;

4) В треугольнике ADC по неравенству треугольника: AD< div>

5) Так как DC=AB, то: AD< div>

6) Разделим обе части неравенства на 2: AD/2<(AC+AB)/2;

7) Так как AM=AD/2, то: AM<(AC+AB)/2, что и требовалось доказать.

Развернуть