Условие:

30. Отрезки АВ и CD пересекаются в точке О. а) Докажите, что сумма расстояний от любой точки плоскости до точек А, В, С и D не меньше чем ОА + ОВ + ОС + OD.

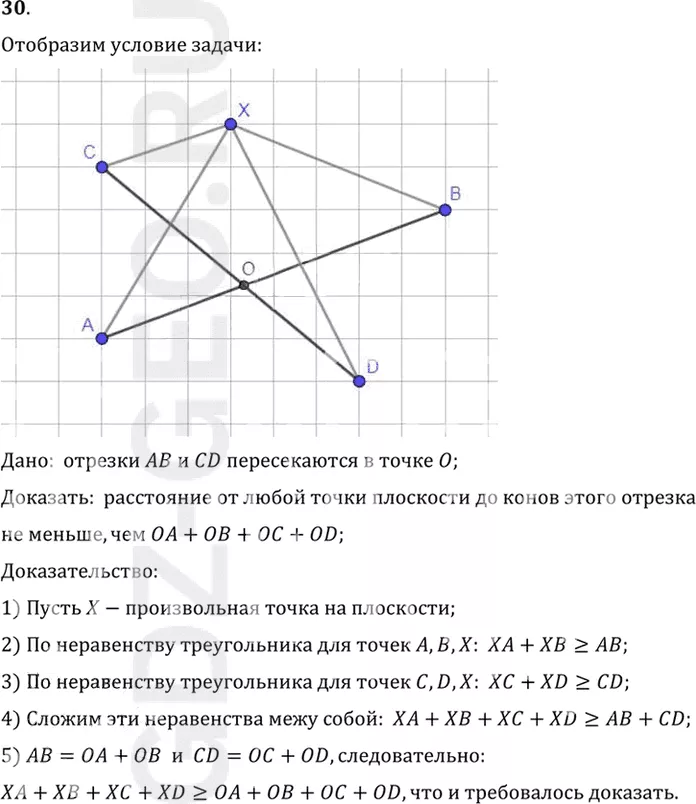
Дано: отрезки AB и CD пересекаются в точке O;

Доказать: расстояние от любой точки плоскости до конов этого отрезка

не меньше, чем OA+OB+OC+OD;

Доказательство:

1) Пусть X-произвольная точка на плоскости;

2) По неравенству треугольника для точек A, B, X: XA+XB>=AB;

3) По неравенству треугольника для точек C, D, X: XC+XD>=CD;

4) Сложим эти неравенства межу собой: XA+XB+XC+XD>=AB+CD;

5) AB=OA+OB и CD=OC+OD, следовательно:

XA+XB+XC+XD>=OA+OB+OC+OD, что и требовалось доказать.

Развернуть