Условие:

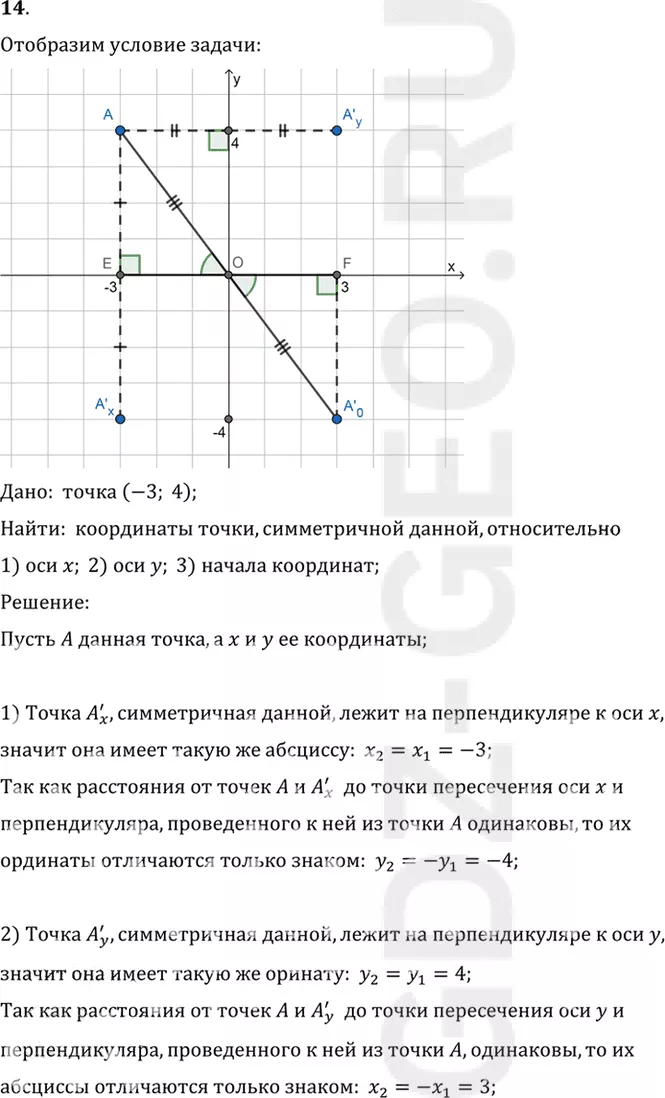
14. Чему равны координаты точки, симметричной точке (-3; 4) относительно: 1) оси х; 2) оси у; 3) начала координат?

Дано: точка (-3; 4);

Найти: координаты точки, симметричной данной, относительно

1) оси x; 2) оси y; 3) начала координат;

Решение:

Пусть A данная точка, а x и y ее координаты;

1) Точка Ax', симметричная данной, лежит на перпендикуляре к оси x,

значит она имеет такую же абсциссу: x2=x1=-3;

Так как расстояния от точек A и Ax' до точки пересечения оси x и

перпендикуляра, проведенного к ней из точки A одинаковы, то их

ординаты отличаются только знаком: y2=-y1=-4;

2) Точка Ay', симметричная данной, лежит на перпендикуляре к оси y,

значит она имеет такую же оринату: y2=y1=4;

Так как расстояния от точек A и Ay' до точки пересечения оси y и

перпендикуляра, проведенного к ней из точки A, одинаковы, то их

абсциссы отличаются только знаком: x2=-x1=3;

3) Точка A0', симметричная данной лежит на прямой OA, при этом

AO=OA0' (по определению симметрии относительно точки);

Опустим перпендикуляры AE и A0' F на ось x;

угол AOE = углу A0' OF (как вертикальные);

Прямоугольные треугольники AOE и A0' OF равны по гипотенузе и

острому углу, отсюда: OF=OE и A0' F=AE;

Значит, абсциссы и ординаты точек A0' и A отличаются только знаком:

x2=-x1=3 и y2=-y1=-4;

Ответ: 1) (-3; -4); 2) (4; -3); 3) (3; -4).

Развернуть