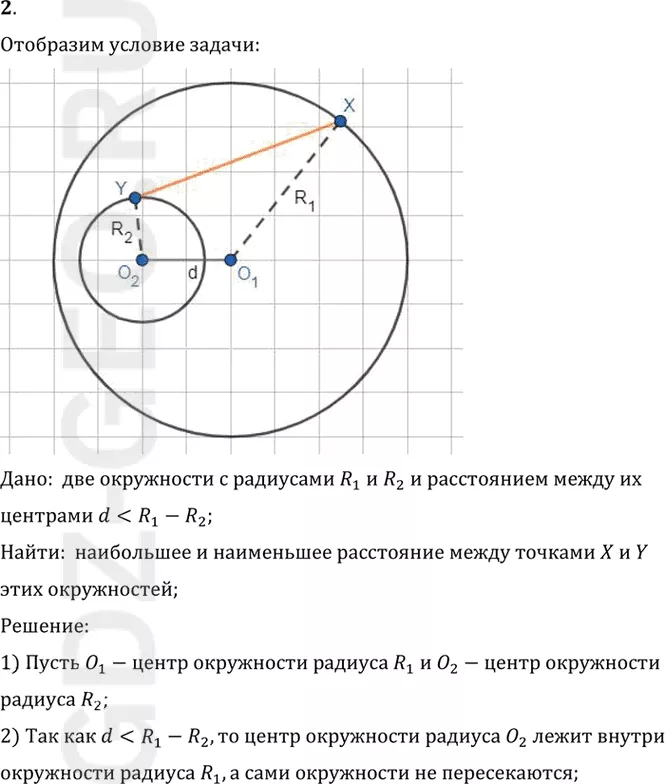
Условие:

2. Решите задачу 1 при условии, что d < R1 - R2 (рис. 293).

Дано: две окружности с радиусами R1 и R2 и расстоянием между их

центрами d< div>

Найти: наибольшее и наименьшее расстояние между точками X и Y

этих окружностей;

Решение:

1) Пусть O1-центр окружности радиуса R1 и O2-центр окружности

радиуса R2;

2) Так как d< div>

окружности радиуса R1, а сами окружности не пересекаются;

3) Пусть X и Y произвольные точки окружностей с центрами O1 и O2

соответственно, тогда для ломаной XYO2 O1 по теореме 13.1:

XO1<=XY+YO2+O2 O1;

R1<=XY+R2+d, отсюда XY >= R1-R2-d;

Значит расстояние R1-R2-d наименьшее;

4) Аналогично для ломаной XO1 O2 Y согласно теореме 13.1:

XY <= XO1+O1 O2+O2 Y => XY <= d+R1+R2;

Значит расстояние d+R1+R2 наибольшее;

Ответ: R1+R2+d; R1-R2-d.

Развернуть