Условие:

8. Докажите, что если четыре прямые, проходящие через точку А, пересекают плоскость а в вершинах параллелограмма, то они пересекают любую плоскость, параллельную а и не проходящую через точку А, тоже в вершинах параллелограмма.

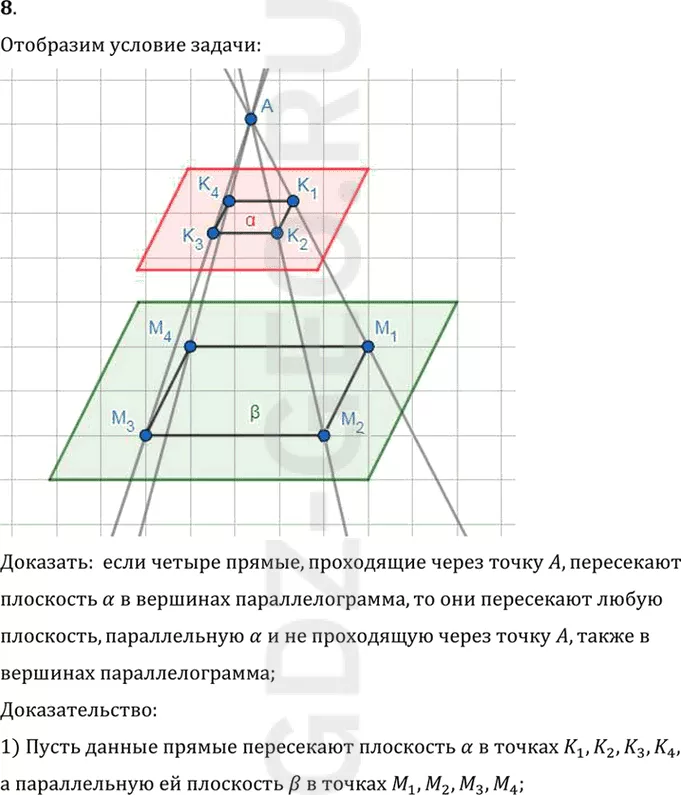
Доказать: если четыре прямые, проходящие через точку A, пересекают

плоскость Альфа в вершинах параллелограмма, то они пересекают любую

плоскость, параллельную Альфа и не проходящую через точку A, также в

вершинах параллелограмма;

Доказательство:

1) Пусть данные прямые пересекают плоскость Альфа в точках K1,K2,K3,K4,

а параллельную ей плоскость Бетта в точках M1,M2,M3,M4;

2) Прямые K1 M1 и K2 M2 пересекаются в точке A, значит через них можно

провести плоскость Гамма;

3) Плоскость Гамма пересекает параллельные плоскости Альфа и Бетта по прямым

K1 K2 и M1 M2,значит эти прямые параллельны: K1 K2||M1 M2;

4) Аналогично доказывается параллельность прямых:

K2 K3||M2 M3,K3 K4||M3 M4 и K1 K4||M1 M4;

5) По условию K1 K2 K3 K4-параллелограмм, значит:

K1 K2||K3 K4 и K2 K3||K1 K4;

6) M1 M2||K1 K2 и K1 K2||K3 K4,значит M1 M2||K3 K4;

7) M3 M4||K3 K4 и M1 M2||K3 K4,значит M1 M2||M3 M4;

8) Аналогично M2 M3||K2 K3,K2 K3||K1 K4 и K1 K4||M1 M4,значит:

M2 M3||M1 M4;

9) Таким образом, четырехугольник M1 M2 M3 M4 является параллелограммом по определению, что и требовалось доказать.