Условие:

9. Даны три параллельные плоскости альфа 1,альфа 2,альфа 3. Пусть Х1,Х2,Х3— точки пересечения этих плоскостей с произвольной прямой.

Докажите, что отношение длин отрезков Х1Х2 : Х2Х3 не зависит от прямой, т. е. одинаково для любых двух прямых.

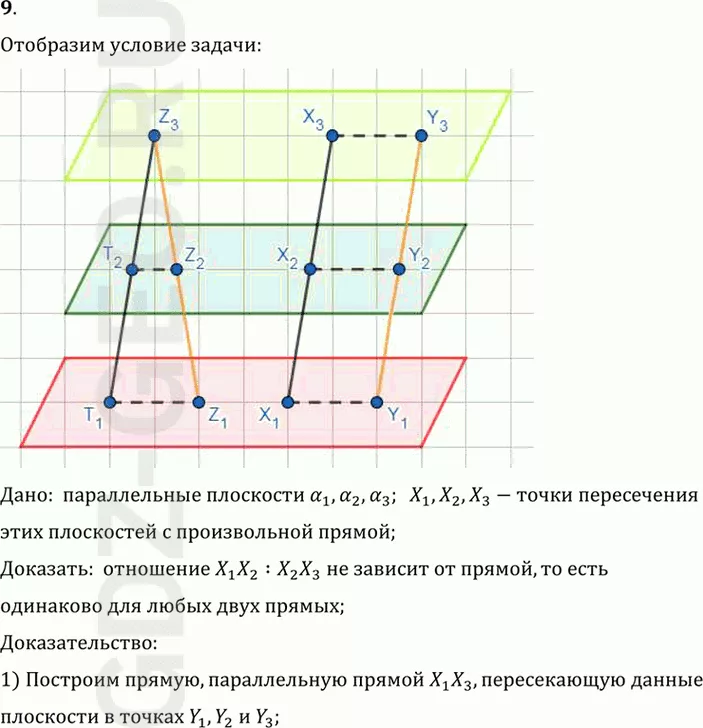
Дано: параллельные плоскости Альфа1,Альфа2,Альфа3; X1,X2,X3-точки пересечения

этих плоскостей с произвольной прямой;

Доказать: отношение X1 X2 :X2 X3 не зависит от прямой, то есть

одинаково для любых двух прямых;

Доказательство:

1) Построим прямую, параллельную прямой X1 X3,пересекающую данные

плоскости в точках Y1,Y2 и Y3;

2) Так как прямые X1 X3 и Y1 Y3 параллельны, то они лежат в одной

плоскости, значит прямые X1 Y1,X2 Y2 и X3 Y3,по которым эта плоскость

пересекает плоскости Альфа1,Альфа2 и Альфа3,параллельны;

3) Четырехугольники X1 Y1 Y2 X2 и X2 Y2 Y3 X3 являются параллелограммами

по определению, значит:

X1 X2=Y1 Y2 и X2 X3=Y2 Y3,отсюда X1 X2 :X2 X3=Y1 Y2 :Y2 Y3;

4) Пусть Z1,Z2 и Z3-точки пересечения произвольной прямой с

плоскостями Альфа1,Альфа2 и Альфа3;

5) Проведем через точку Z3 прямую, параллельную прямой X1 X3,и

пересекающую плоскости Альфа1 и Альфа2 в точках T1 и T2 по доказанному:

T1 T2 :T2 Z3=X1 X2 :X2 X3;

6) Так как прямые Z1 Z3 и T1 Z3 пересекаются, то через них можно

провести плоскость, значит прямые Z1 T1 и Z2 T2,по которым эта плоскость

пересекает плоскости Альфа1 и Альфа2,параллельны;

7) По теореме о пропорциональных отрезках:

Z1 Z2 :Z2 Z3=T1 T2 :T2 Z3=X1 X2 :X2 X3,что и требовалось доказать.

Развернуть