Условие:

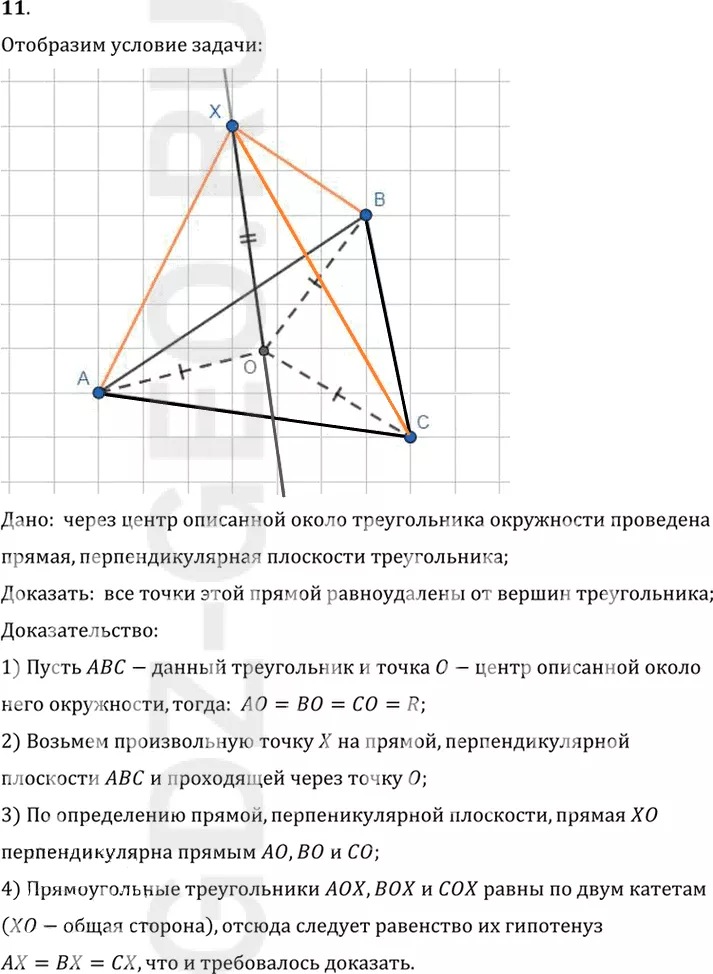
11. Через центр описанной около треугольника окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от вершин треугольника.

Дано: через центр описанной около треугольника окружности проведена

прямая, перпендикулярная плоскости треугольника;

Доказать: все точки этой прямой равноудалены от вершин треугольника;

Доказательство:

1) Пусть ABC-данный треугольник и точка O-центр описанной около

него окружности, тогда: AO=BO=CO=R;

2) Возьмем произвольную точку X на прямой, перпендикулярной

плоскости ABC и проходящей через точку O;

3) По определению прямой, перпеникулярной плоскости, прямая XO

перпендикулярна прямым AO, BO и CO;

4) Прямоугольные треугольники AOX, BOX и COX равны по двум катетам

(XO-общая сторона), отсюда следует равенство их гипотенуз

AX=BX=CX, что и требовалось доказать.