Условие:

14. Верхние концы двух вертикально стоящих столбов, удалённых на расстояние 3,4 м, соединены перекладиной. Высота одного столба 5,8 м, а другого — 3,9 м. Найдите длину перекладины.

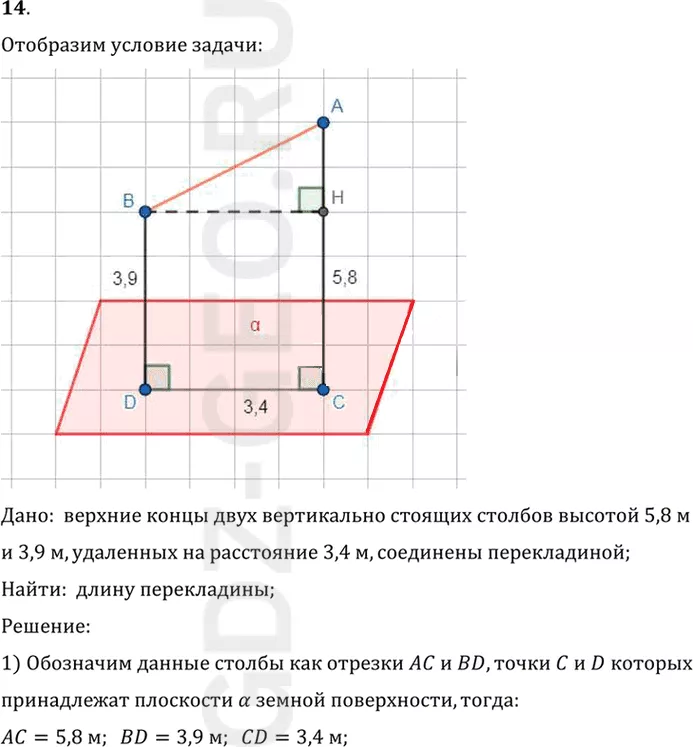
Дано: верхние концы двух вертикально стоящих столбов высотой 5,8 м

и 3,9 м, удаленных на расстояние 3,4 м, соединены перекладиной;

Найти: длину перекладины;

Решение:

1) Обозначим данные столбы как отрезки AC и BD, точки C и D которых

принадлежат плоскости Альфа земной поверхности, тогда:

AC=5,8 м; BD=3,9 м; CD=3,4 м;

2) Так как столбы стоят вертикально, то AC перпендикулярен a и BD перпендикулярен a, следовательно:

AC перпендикулярен CD, BD перпендикулярен CD и AC||BD;

3) Значит прямые AC и BD и все их точки лежат в одной плоскости;

4) Четырехугольник ACDB является прямоугольной трапецией;

5) Опустим высоту BH на сторону AC, тогда:

CD перпендикулярен AC и BH перпендикулярен AC, значит BH||CD;

6) Четырехугольник ACDH-параллелограмм, значит:

BH=CD=3,4 м и HC=BD=3,9 м;

7) AH=AC-HC=5,8-3,9=1,9 м;

8) В прямоугольном треугольнике AHB, по теореме Пифагора:

AB=v(AH^2+BH^2 )=v(1,9^2+3,4^2 )=v(3,61+11,56)=v15,17=3,9 м;

Ответ: 3,9 м.

Развернуть