Условие:

25. Докажите, что любая сторона треугольника больше разности двух других его сторон.

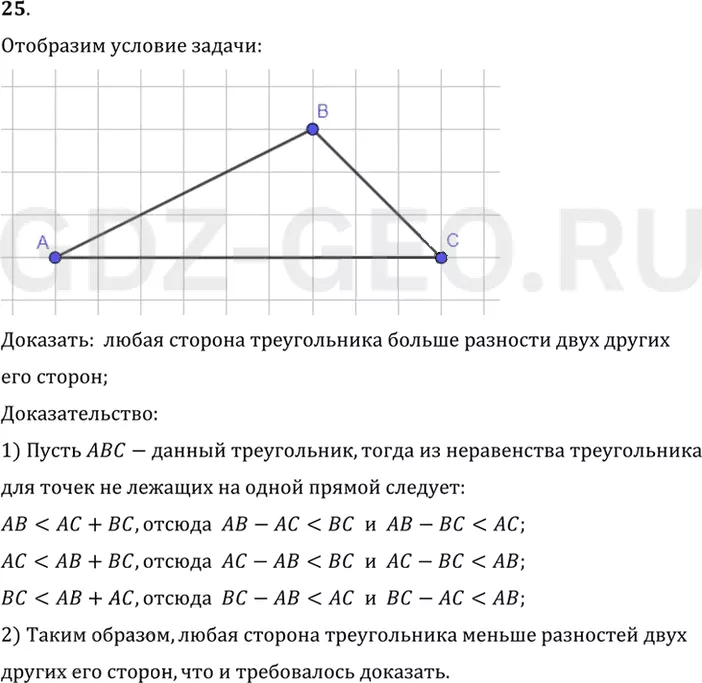
Доказать: любая сторона треугольника больше разности двух других

его сторон;

Доказательство:

1) Пусть ABC-данный треугольник, тогда из неравенства треугольника

для точек не лежащих на одной прямой следует:

AB< div>

AC< div>

BC< div>

2) Таким образом, любая сторона треугольника меньше разностей двух

других его сторон, что и требовалось доказать.

Развернуть