Условие:

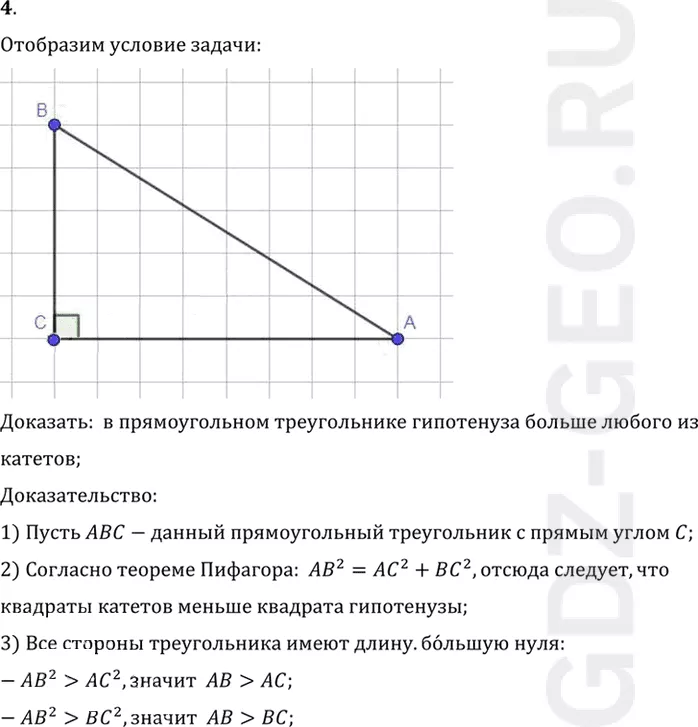
4. Докажите, что в прямоугольном треугольнике гипотенуза больше любого из катетов.

Доказать: в прямоугольном треугольнике гипотенуза больше любого из

катетов;

Доказательство:

1) Пусть ABC-данный прямоугольный треугольник с прямым углом C;

2) Согласно теореме Пифагора: AB^2=AC^2+BC^2, отсюда следует, что

квадраты катетов меньше квадрата гипотенузы;

3) Все стороны треугольника имеют длину, большую нуля:

- AB^2>AC^2, значит AB>AC;

- AB^2>BC^2, значит AB>BC;

Развернуть