Условие:

3. Докажите теорему Пифагора.

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы

равен сумме квадратов катетов;

Доказательство:

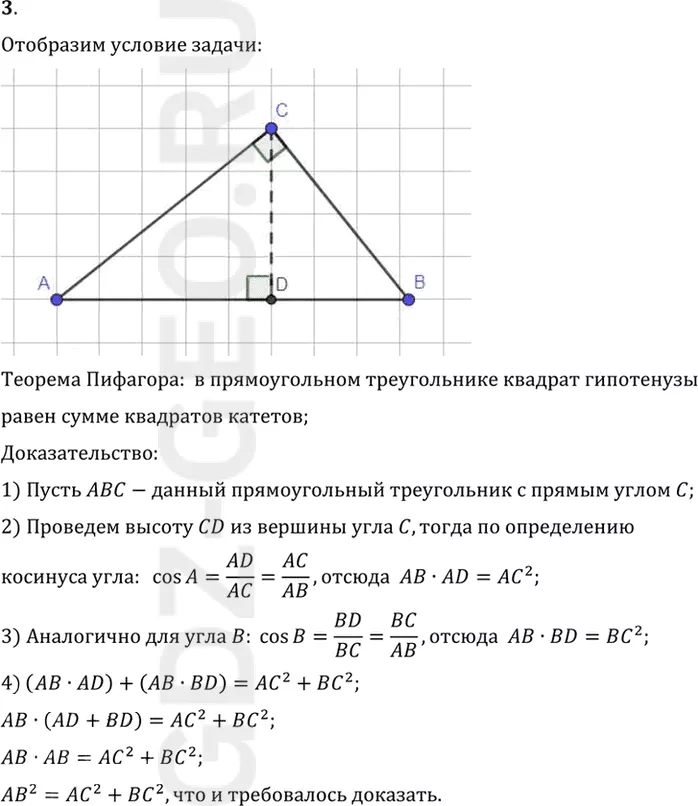
1) Пусть ABC-данный прямоугольный треугольник с прямым углом C;

2) Проведем высоту CD из вершины угла C, тогда по определению

косинуса угла: cosA=AD/AC=AC/AB, отсюда AB•AD=AC^2;

3) Аналогично для угла B: cosB=BD/BC=BC/AB, отсюда AB•BD=BC^2;

4) (AB•AD)+(AB•BD)=AC^2+BC^2;

AB•(AD+BD)=AC^2+BC^2;

AB•AB=AC^2+BC^2;

AB^2=AC^2+BC^2, что и требовалось доказать.

Развернуть