Условие:

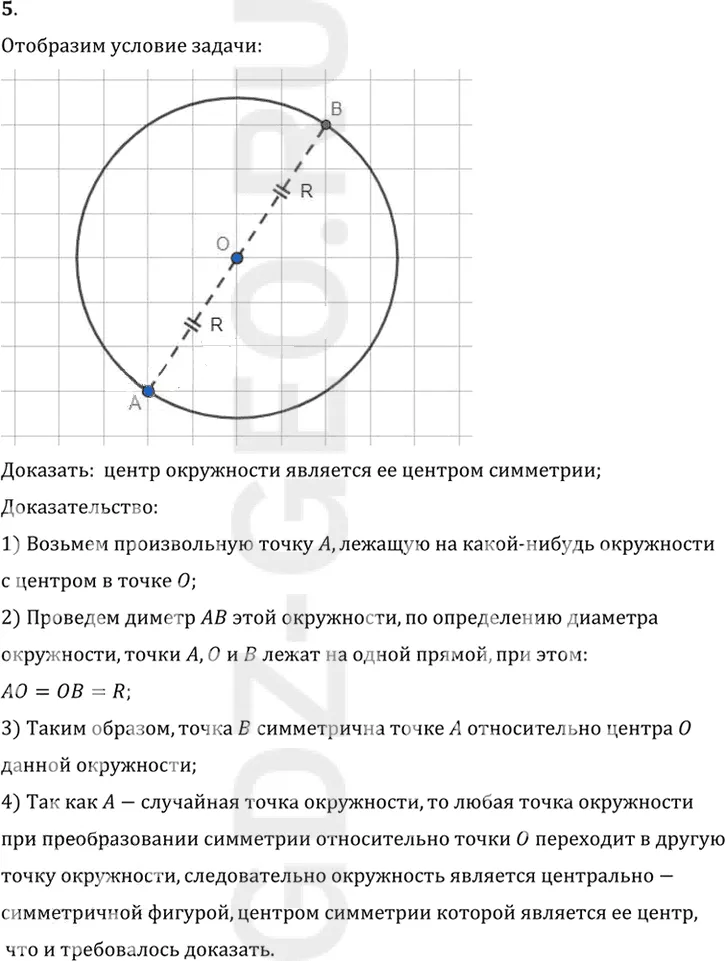
5. Докажите, что центр окружности является её центром симметрии.

Доказать: центр окружности является ее центром симметрии;

Доказательство:

1) Возьмем произвольную точку A, лежащую на какой-нибудь окружности

с центром в точке O;

2) Проведем диметр AB этой окружности, по определению диаметра

окружности, точки A, O и B лежат на одной прямой, при этом:

AO=OB=R;

3) Таким образом, точка B симметрична точке A относительно центра O

данной окружности;

4) Так как A-случайная точка окружности, то любая точка окружности

при преобразовании симметрии относительно точки O переходит в другую

точку окружности, следовательно окружность является центрально-

симметричной фигурой, центром симметрии которой является ее центр,

что и требовалось доказать.

Развернуть