Условие:

8. Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии.

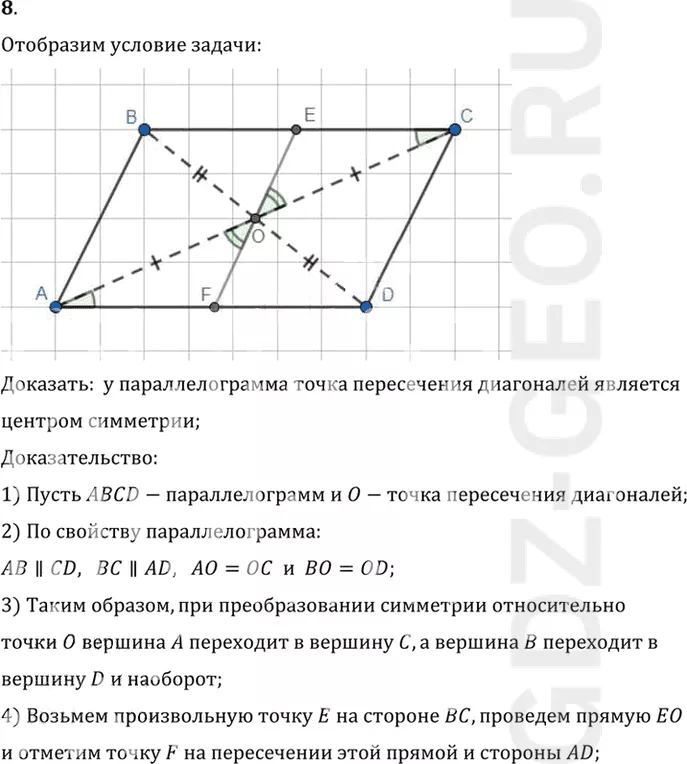
Доказать: у параллелограмма точка пересечения диагоналей является

центром симметрии;

Доказательство:

1) Пусть ABCD-параллелограмм и O-точка пересечения диагоналей;

2) По свойству параллелограмма:

AB||CD, BC||AD, AO=OC и BO=OD;

3) Таким образом, при преобразовании симметрии относительно

точки O вершина A переходит в вершину C, а вершина B переходит в

вершину D и наоборот;

4) Возьмем произвольную точку E на стороне BC, проведем прямую EO

и отметим точку F на пересечении этой прямой и стороны AD;

5) Углы AOF и EOC равны как вертикальные;

6) Углы OAF и OCE равны как внутренние накрест лежащие при

параллельных прямых AD и BC и секущей EF;

7) Треугольники AOF и COE равны по второму признаку, отсюда

OE=OF, следовательно точки E и F симметричны относительно

точки O;

8) Аналогично, доказывается что произвольная точка стороны AB

переходит в точку стороны CD;

9) Таким образом, каждая точка параллелограмма при преобразовании

симметрии относительно точки пересечения его диагоналей переходит

в другую точку параллелограмма, следовательно параллелограмм

является центрально-симметричной фигурой с центром симметрии в

точке пересечения диагоналей, что и требовалось доказать.

Развернуть