Условие:

11. Что представляет собой фигура, симметричная относительно данной точки: 1) отрезку; 2) углу; 3) треугольнику?

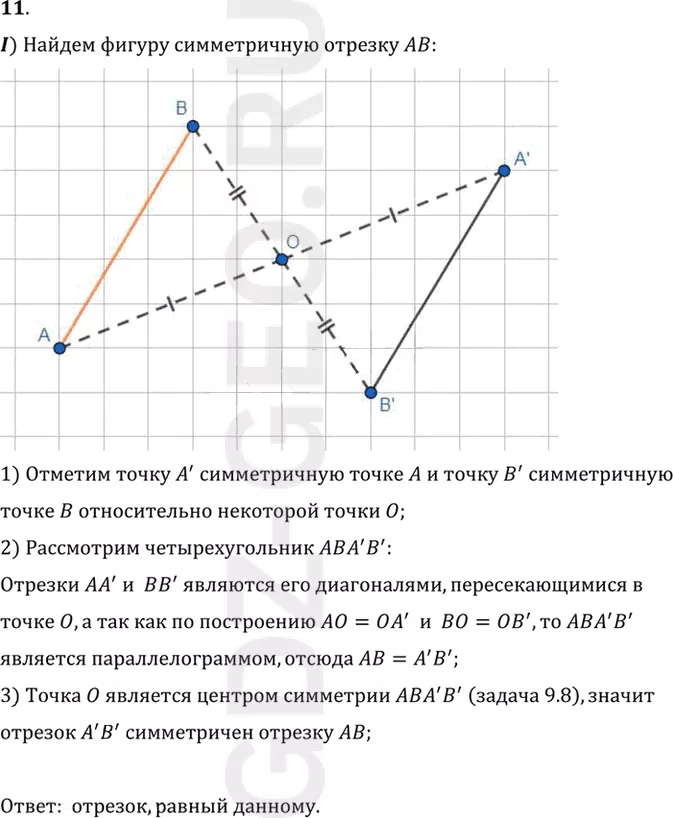
I) Найдем фигуру симметричную отрезку AB.

1) Отметим точку A' симметричную точке A и точку B' симметричную

точке B относительно некоторой точки O;

2) Рассмотрим четырехугольник ABA' B':

Отрезки AA' и BB' являются его диагоналями, пересекающимися в

точке O, а так как по построению AO=OA' и BO=OB', то ABA' B'

является параллелограммом, отсюда AB=A' B';

3) Точка O является центром симметрии ABA' B' (задача 9.8), значит

отрезок A' B' симметричен отрезку AB;

Ответ: отрезок, равный данному.

II) Найдем фигуру симметричную углу O.

1) Отметим произвольные точки A и B на сторонах угла O;

2) Отметим точки A', O' и B' симметричные точкам A, O и B относительно некоторой точки S;

3) Отрезки A' O', O' B' и A' B' соответственно симметричны и равны

отрезкам AO, OB и AB;

4) Так как точки A и B на сторонах угла AOB произвольные, то любые

точки на сторонах угла AOB симметричны каким-нибудь точкам на

сторонах угла A' O' B', следовательно эти углы симметричны;

5) Треугольники A' O' B' и AOB равны по третьему признаку, отсюда

угол A' O' B' = углу AOB;

Ответ: угол, равный данному.

III) Найдем фигуру симметричную треугольнику ABC.

1) Отметим точки A', B' и C' симметричные точкам A, B и C относи-

тельно некоторой точки O;

2) Отрезки A' B', B' C' и A' C' соответственно симметричны и равны

отрезкам AB, BC и AC, значит треугольники A' B' C' и ABC симметричны;

3) Треугольники A' B' C' и ABC равны по третьему признаку;

Ответ: треугольник, равный данному.

Развернуть