Условие:
5.414. Найдите значение выражения:
а) 23/30 - (1/6 + 2/5); б) 11/42 + (3/7 - 1/6);
в) 11/15 - (2/3 - 3/5); г) 5/18 + (2/9 + 1/2).
Порядок выполнения действий выбираем согласно следующему правилу – если в выражении есть скобки, то сначала выполняют действия в скобках, причём, как в скобках, так и за скобками, сначала выполняют умножение и деление по порядку слева направо, а потом сложение и вычитание также по порядку слева направо.
Согласно основному свойству дроби, если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
а) 23/30-(1/6+2/5)=23/30-((1•5)/(6•5)+(2•6)/(5•6))=23/30-(5/30+12/30)=23/30-(5+12)/30=23/30-17/30=(23-17)/30=6/30=(1•6)/(5•6)=1/5
б) 11/42+(3/7-1/6)=11/42+((3•6)/(7•6)-(1•7)/(6•7))=11/42+(18/42-7/42)=11/42+(18-7)/42=11/42+11/42=(11+11)/42=22/42=(2•11)/(2•21)=11/21
в) 11/15-(2/3-3/5)=11/15-((2•5)/(3•5)-(3•3)/(5•3))=11/15-(10/15-9/15)=11/15-(10-9)/15=11/15-1/15=(11-1)/15=10/15=(2•5)/(3•5)=2/3
г) 5/18+(2/9+1/2)=5/18+((2•2)/(9•2)+(1•9)/(2•9))=5/18+(4/18+9/18)=5/18+(4+9)/15=5/18+13/18=(5+13)/18=18/18=1
Решение 1 - 5.414 - §5 Обыкновенные дроби:
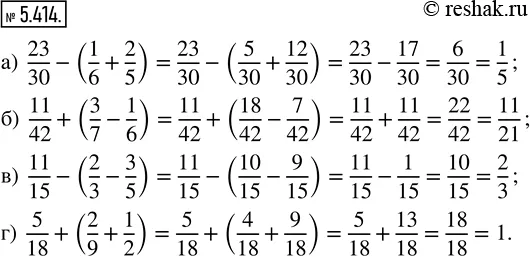
Решение 2 - 5.414:

