Условие:
5.416. Найдите корень уравнения:
а) 1/3 + x = 5/6; в) x + 4/18 = 5/6 + 1/3;
б) x - 2/5 = 3/10; г) (9/10 - x) + 9/15 = 1.
Согласно основному свойству дроби, если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь.
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
а) 1/3+x=5/6
В уравнении неизвестно слагаемое x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
x=5/6-1/3
x=5/6-(1•2)/(3•2)
x=5/6-2/6
x=(5-2)/6
Или, выполнив вычитание
x=3/6
x=(3•1)/(3•2)=1/2
б) x-2/5=3/10
В уравнении неизвестно уменьшаемое x.
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим
x=3/10+2/5
x=3/10+(2•2)/(5•2)
x=3/10+4/10
x=(3+4)/10
Или, выполнив сложение
x=7/10
в) x+4/15=2/3+2/5
Выполним сложение в правой части уравнения.
x+4/15=(2•5)/(3•5)+(2•3)/(5•3)
x+4/15=10/15+6/15
x+4/15=(10+6)/15
x+4/15=16/15
В уравнении неизвестно слагаемое x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
x=16/15-4/15
x=(16-4)/15
Или, выполнив вычитание, получим
x=12/15
г) (4/5-x)+13/20=25/30
Решим уравнение относительно сложения, то есть неизвестно слагаемое 4/5-x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
4/5-x=25/30-13/20
4/5-x=(25•2)/(30•2)-(13•3)/(20•3)
4/5-x=50/60-39/60
4/5-x=(50-39)/60
Или, выполнив вычитание
4/5-x=11/60
Теперь решаем уравнение относительно вычитания, то есть неизвестно вычитаемое x.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
x=4/5-11/60
x=(4•12)/(5•12)-11/60
x=48/60-11/60
x=(48-11)/60
Или, выполнив вычитание,
x=37/60
Решение 1 - 5.416 - §5 Обыкновенные дроби:
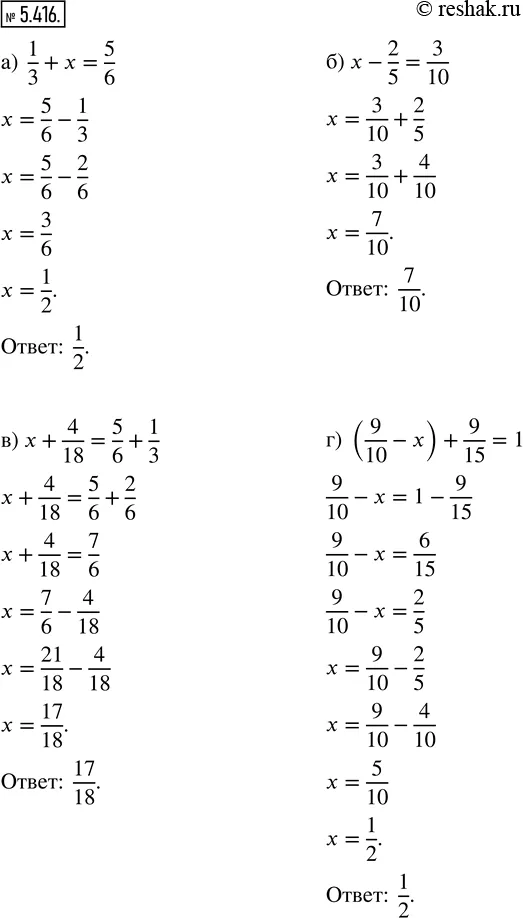
Решение 2 - 5.416:

Решение 3 - 5.416:

Решение 4 - 5.416:

